Contourner les conflits
En explorant le graphe, il arrive souvent de tomber sur des situations qui mèneraient à des conflits. Il faut être en mesure de rajouter du délai pour les éviter.
Décalage du temps de départ
Dans les paramètres de l’algorithme, le temps de départ est donné sous la forme d’une fenêtre : un temps de départ au plus tôt et au plus tard. Tant que c’est possible, il est toujours préférable de décaler le temps de départ pour éviter les conflits.
Par exemple : un train doit partir entre 10:00 et 11:00. En partant à 10:00, cela provoque un conflit, le train doit entrer en gare d’arrivée 15 minutes plus tard. Il suffit de faire partir le train à 10:15 pour régler le problème.
Dans OSRD, cette fonctionnalité est gérée en gardant une trace, à chaque arête, du décalage maximal du temps de départ qui pourra être ajouté sur la suite du parcours. Tant que cette valeur est suffisante, tous les conflits sont évités par ce moyen.
Le décalage du temps de départ est une valeur stockée sur chaque arête et additionnée à la fin de la recherche de chemin.
Par exemple :
- un train doit partir entre 10:00 et 11:00. La recherche commence avec un délai maximal de 1:00.
- Après quelques arêtes, une non-disponibilité est constatée 20 minutes après notre passage. La valeur passe donc à 20 minutes pour la suite du parcours.
- Le temps de départ est ensuite décalé de 5 minutes pour contourner un conflit, modifiant le décalage maximal à 15 minutes.
- Ce procédé continue jusqu’à arriver à la fin du trajet, ou jusqu’au point où il faut ajouter plus de délai.
Marges de construction
Quand la valeur de décalage maximal du temps de départ tombe à 0, il faut rajouter du délai entre deux points du parcours du train.
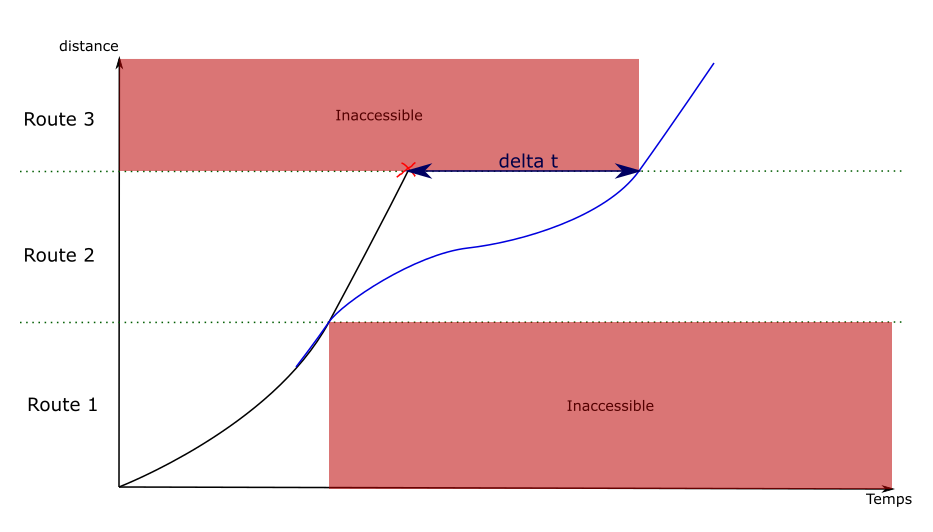
Le principe est le même que pour régler les discontinuités de vitesse : le graphe est parcouru en arrière pour créer de nouvelles arêtes.
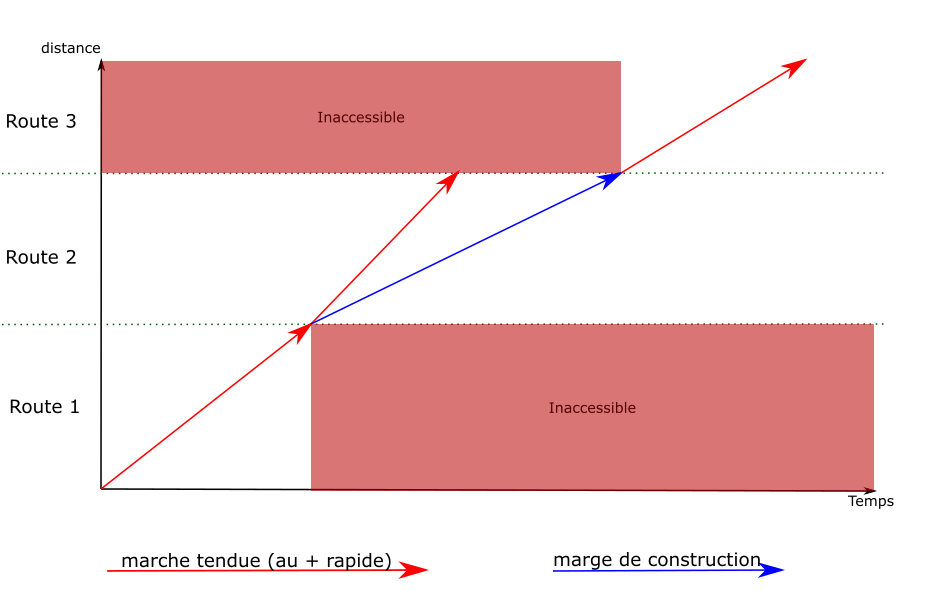
La marge de construction est une fonctionnalité du calcul de marche permettant d’ajouter un délai donné entre deux points du parcours.
Post-processing
Les marges de constructions étaient calculées pendant l’exploration du graph, mais ce procédé était trop couteux en temps de calcul. On effectuait des dichotomies sur des simulations qui pouvaient s’étendre sur des portions importantes du chemin.
On a seulement besoin de savoir si la marge de construction peut être réalisée sans provoquer de conflit. Des heuristiques peuvent être utilisées ici tant qu’on est plus restrictif que permissif : une marge impossible doit être identifiée comme telle, mais manquer une solution avec une marge extrêmement serrée n’est pas une mauvaise chose.
Mais avec ce changement, une fois qu’une solution est trouvée, il ne suffit plus de concaténer les résultats de simulation pour obtenir la simulation finale. On doit réaliser une simulation complète avec les vraies marges de construction qui évitent tout conflit. Cette étape se rejoint avec celle décrite pour les marges de régularité, qui est maintenant réalisée même sans marge de régularité spécifiée.