Module de recherche de sillons

• 1: Parcours de l'infrastructure
• 2: Détection de conflits
• 3: Représentation de l'espace de solutions
• 4: Discontinuités et retours en arrière
• 5: Contourner les conflits
• 6: Marge de régularité
• 7: Détails d'implémentation

1 - Parcours de l'infrastructure

La première chose à définir est comment un train se déplace sur l’infrastructure, sans prendre en compte les conflits pour l’instant.

On a besoin d’une manière de définir et d’énumérer les différents chemins possibles et de parcourir l’infrastructure, avec plusieurs contraintes :

1. Le chemin doit être compatible avec le matériel roulant donné (électrification, gabarit, systèmes de signalisation)
2. À n’importe quel point, on doit être en mesure d’accéder aux propriétés du chemin depuis le point de départ jusqu’au point considéré. Cela inclus les routes et les cantons.
3. Dans certains cas, on doit savoir où le train ira après le point actuellement évalué (pour une détection de conflits correcte).

Pour répondre à ce besoin, une classe InfraExplorer a été implémentée. Elle utilise les cantons (section de signal en signal) comme subdivision principale. Elle est composée de 3 sections : le canton courant, les prédécesseurs, et les cantons suivants.

Dans cet exemple, les flèches vertes sont les cantons précédents. Ce qui se produit dessus est considéré comme immuable.

La flèche rouge est le canton actuellement exploré. C’est à cet endroit que les simulations du train et de la signalisation sont effectuées, et que les conflits sont évités.

Les flèches bleues sont les cantons suivants. Cette section n’est pas encore simulée, elle existe seulement pour savoir où le train ira ensuite. Dans cet exemple, elle indique que le signal en bas à droite peut être ignoré, seul le chemin du haut sera utilisé. Le chemin du bas sera évalué dans une autre instance de InfraExplorer.

Plus de détails sur la classe et son interface sont présents sur la version anglaise de la page.

2 - Détection de conflits

Maintenant qu’on sait quels chemins peuvent être utilisés, on doit déterminer à quel moment ces chemins sont libres.

La documentation (en anglais seulement) de la détection de conflits explique comment elle est réalisée en interne. Pour résumer, un train est en conflit avec un autre quand il observe un signal lui indiquant de ralentir. Dans notre cas, une solution où cette situation se produit est considérée comme invalide, le train doit arriver au signal donné plus tard (ou plus tôt) quand le signal n’est plus contraignant.

Cependant, la détection de conflit doit être réalisée de manière incrémentale, ce qui veut dire que :

1. Quand une simulation est effectuée jusqu’à t=x, tous les conflits qui arrivent avant t=x doivent être connus, même s’ils sont indirectement provoqués par un signal vu à t > x plus loin sur le chemin.
2. Les conflits et utilisations de ressources doivent être identifiés dès qu’ils se produisent, même si le temps de fin d’utilisation n’est pas encore défini.

Pour que ce soit possible, on doit être en mesure de savoir où le train ira après la section actuellement simulée (cf exploration de l’infrastructure )

Pour gérer ce cas, le module de détection de conflit peut renvoyer une erreur quand il est nécessaire d’avoir plus d’information sur la suite du chemin. Quand ce cas se produit, les objets InfraExplorer sont clonés pour étendre les chemins.

3 - Représentation de l'espace de solutions

Principe général

Le problème reste une recherche de graphe. En représentant l’espace de solution sous forme de graphe, il est possible de réutiliser nos outils déjà existants de recherche de chemin.

Le graphe produit de la position, du temps, et de la vitesse est utilisé. Autrement dit, chaque élément du graphe contient (entre autres) ces 3 variables.

Chaque arête du graphe est calculée avec un calcul de marche pour connaître l’évolution de la vitesse et de la position dans le temps.

Représentation visuelle

Le graphe de départ représente l’infrastructure physique

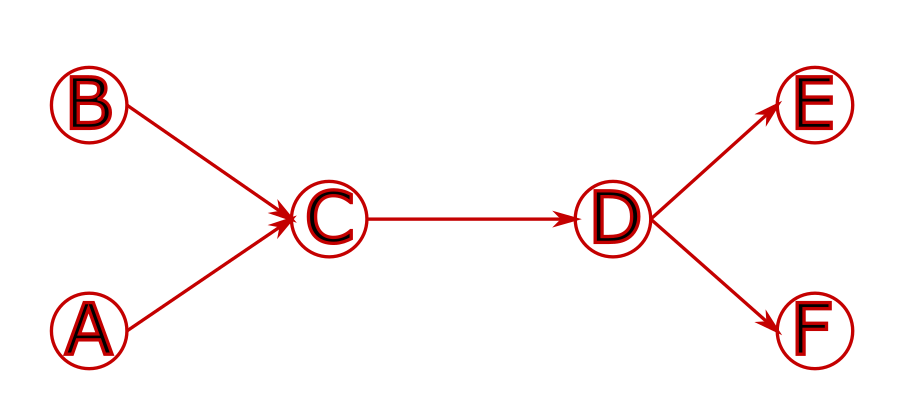
Il est ensuite “dupliqué” à des temps différents

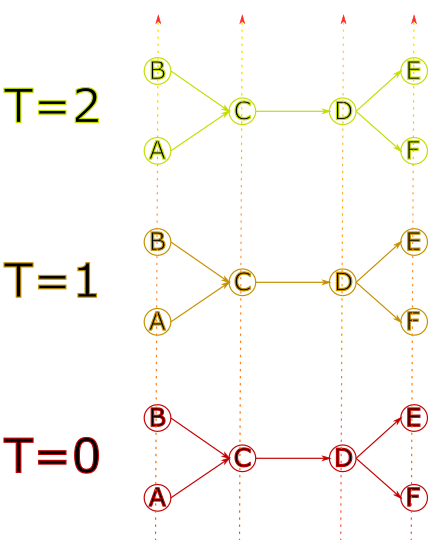
Puis des nœuds sont reliés de manière à refléter le temps de parcours

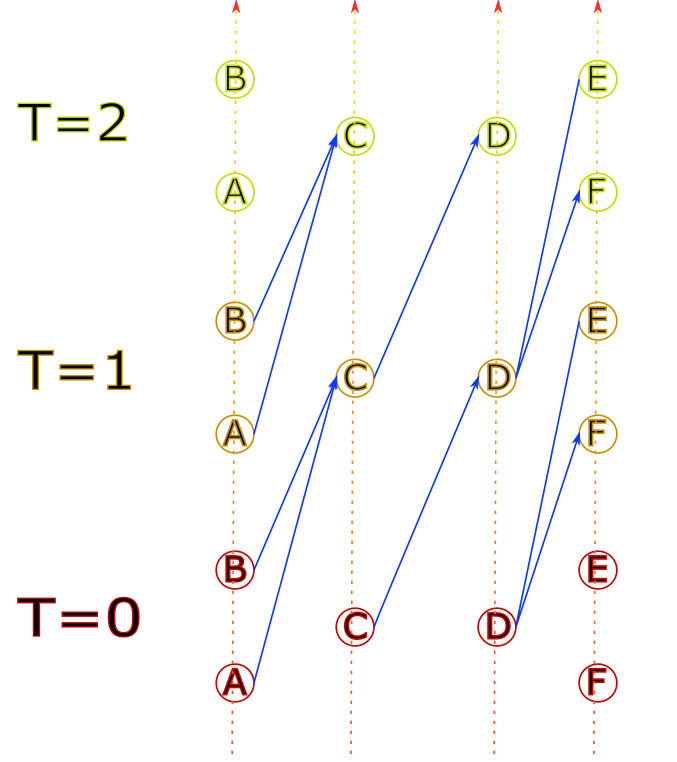
Précisions

• Le graphe est construit au fil de l’exploration.
• Une discrétisation est faite au niveau du temps, uniquement pour évaluer ce qui a déjà été visité. Si le même emplacement est visité une seconde fois, il faut une certaine différence de temps pour estimer qu’il n’est pas déjà visité.
• Toutes les arêtes sont réalisées avec des calculs de marche
• La vitesse n’est pas discrétisée ni utilisée pour estimer quel emplacement est déjà visité, mais elle fait partie des calculs.
• Par défaut, tous les calculs sont faits en allant à la vitesse maximale. Les ralentissements sont ajoutés seulement quand ils sont nécessaires.

Exemple

Par exemple, avec l’infrastructure suivante en se basant sur le graphe des voies :

Explorer le graphe des sillons possibles peut donner ce type de résultat :

4 - Discontinuités et retours en arrière

Le problème des discontinuités

Au moment d’explorer une arête du graphe, on effectue un calcul de marche pour connaître l’évolution de la vitesse. Mais il n’est pas possible de voir plus loin que l’arête en question, ce qui est gênant pour calculer les courbes de freinages qui peuvent nécessiter de commencer à freiner plusieurs kilomètres avant l’arrivée.

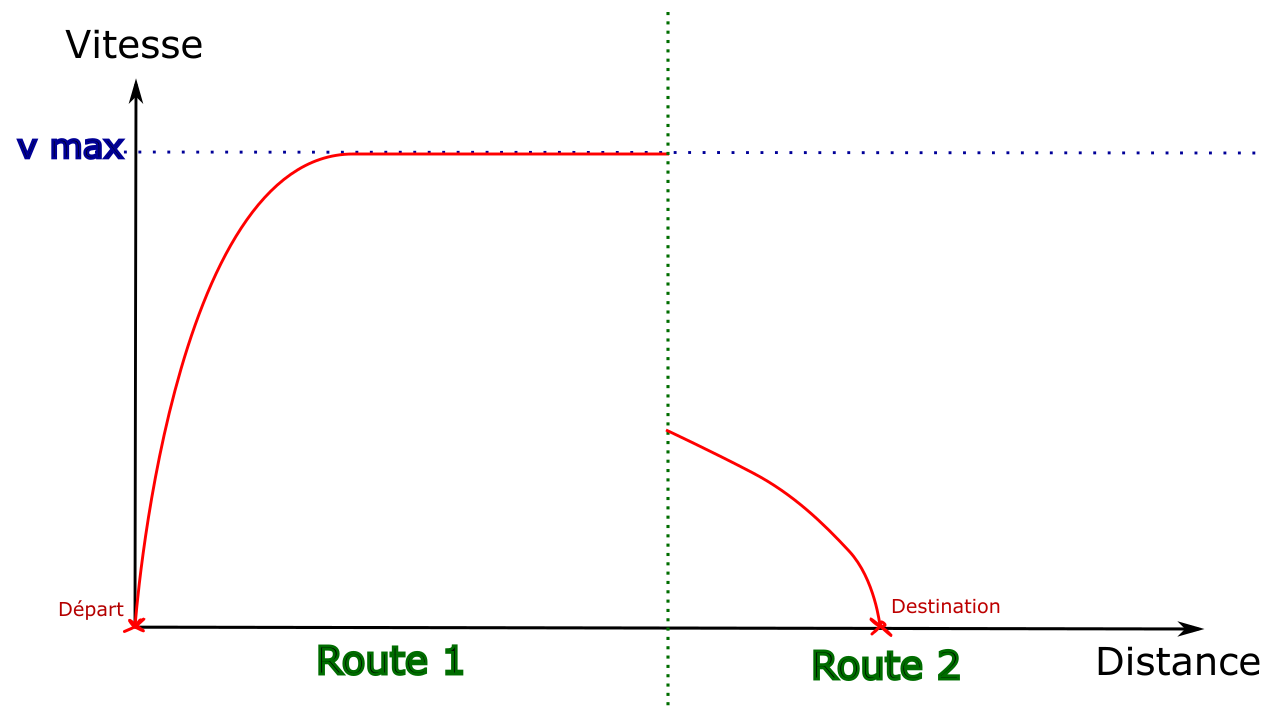
Cet exemple illustre le problème : par défaut la première arête est explorée en allant à la vitesse maximale. C’est seulement en explorant la seconde arête que la destination devient visible, sans que la distance restante soit suffisante pour s’arrêter.

La solution : revenir en arrière

Pour régler ce problème, lorsqu’une arête est générée avec une discontinuité dans les courbes de vitesse, l’algorithme revient sur les arêtes précédentes pour en créer des nouvelles qui incluent les décélérations.

Pour donner un exemple simplifié, sur un chemin de 4 routes où le train peut accélérer ou décélérer de 10km/h par route :

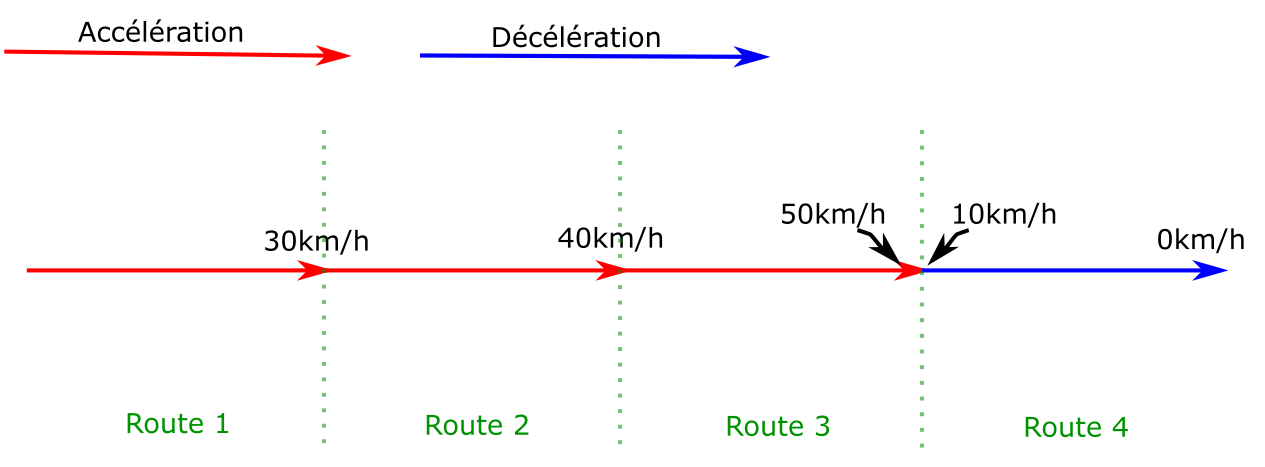
Pour que le train s’arrête à la fin de la route 4, il doit être au plus à 10km/h à la fin de la route 3. Une nouvelle arête est alors créée sur la route 3 qui finit à 10km/h. Une décélération est ensuite calculée à rebours de la fin de la route vers le début, jusqu’à retrouver la courbe d’origine (ou le début de l’arrête).

Dans cet exemple, la discontinuité a seulement été déplacée vers la transition entre les routes 2 et 3. Le procédé est ensuite réitéré sur la route 2, ce qui donne le résultat suivant :

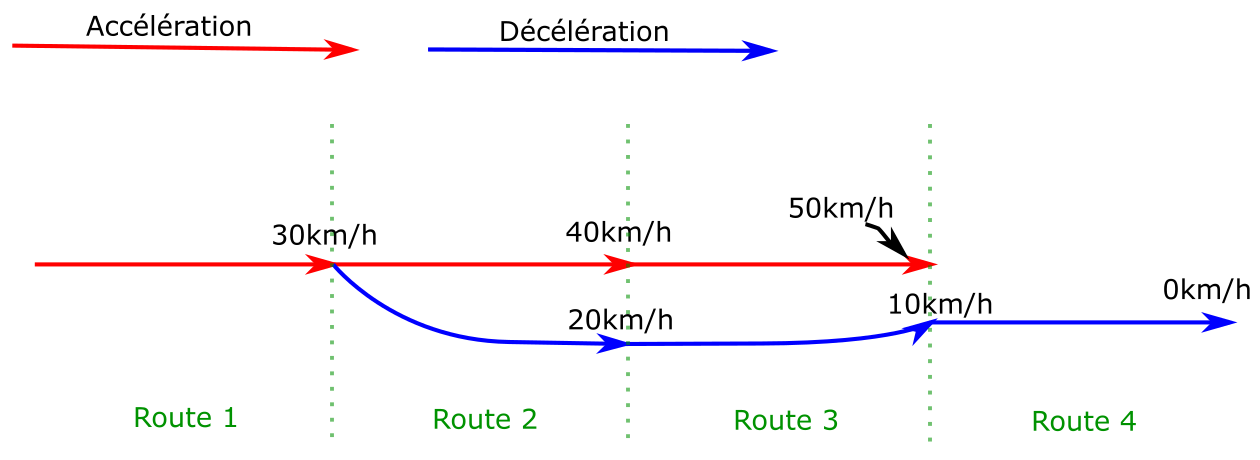
Les anciennes arêtes sont toujours présentes dans le graphe, elles peuvent mener à d’autres solutions.

5 - Contourner les conflits

En explorant le graphe, il arrive souvent de tomber sur des situations qui mèneraient à des conflits. Il faut être en mesure de rajouter du délai pour les éviter.

Décalage du temps de départ

Dans les paramètres de l’algorithme, le temps de départ est donné sous la forme d’une fenêtre : un temps de départ au plus tôt et au plus tard. Tant que c’est possible, il est toujours préférable de décaler le temps de départ pour éviter les conflits.

Par exemple : un train doit partir entre 10:00 et 11:00. En partant à 10:00, cela provoque un conflit, le train doit entrer en gare d’arrivée 15 minutes plus tard. Il suffit de faire partir le train à 10:15 pour régler le problème.

Dans OSRD, cette fonctionnalité est gérée en gardant une trace, à chaque arête, du décalage maximal du temps de départ qui pourra être ajouté sur la suite du parcours. Tant que cette valeur est suffisante, tous les conflits sont évités par ce moyen.

Le décalage du temps de départ est une valeur stockée sur chaque arête et additionnée à la fin de la recherche de chemin.

Par exemple :

• un train doit partir entre 10:00 et 11:00. La recherche commence avec un délai maximal de 1:00.
• Après quelques arêtes, une non-disponibilité est constatée 20 minutes après notre passage. La valeur passe donc à 20 minutes pour la suite du parcours.
• Le temps de départ est ensuite décalé de 5 minutes pour contourner un conflit, modifiant le décalage maximal à 15 minutes.
• Ce procédé continue jusqu’à arriver à la fin du trajet, ou jusqu’au point où il faut ajouter plus de délai.

Marges de construction

Quand la valeur de décalage maximal du temps de départ tombe à 0, il faut rajouter du délai entre deux points du parcours du train.

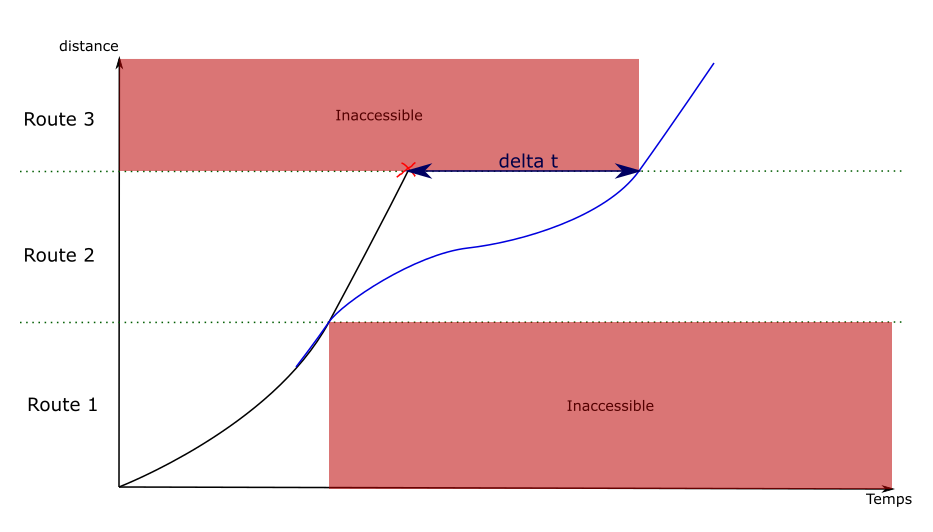
Le principe est le même que pour régler les discontinuités de vitesse : le graphe est parcouru en arrière pour créer de nouvelles arêtes.

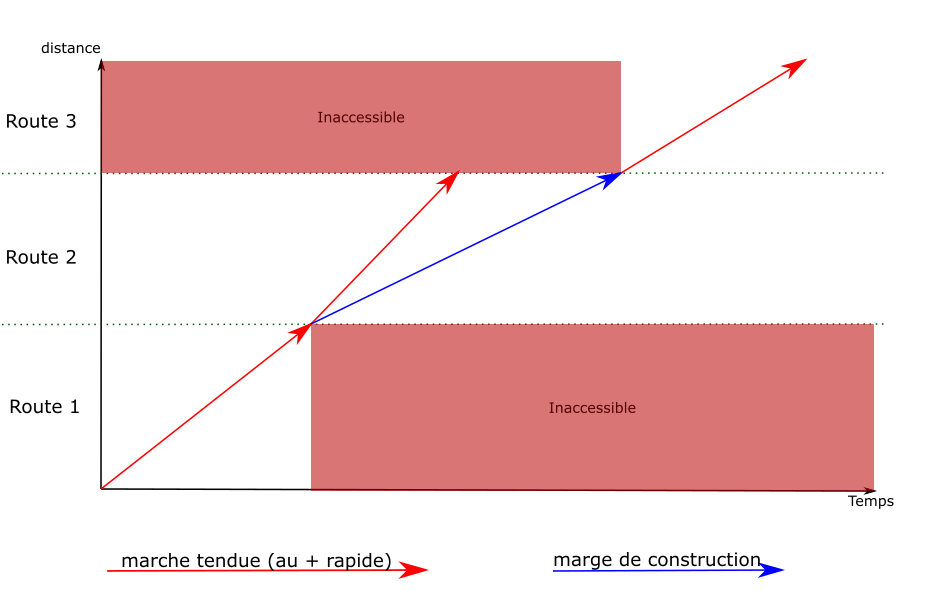
La marge de construction est une fonctionnalité du calcul de marche permettant d’ajouter un délai donné entre deux points du parcours.

Post-processing

Les marges de constructions étaient calculées pendant l’exploration du graph, mais ce procédé était trop couteux en temps de calcul. On effectuait des dichotomies sur des simulations qui pouvaient s’étendre sur des portions importantes du chemin.

On a seulement besoin de savoir si la marge de construction peut être réalisée sans provoquer de conflit. Des heuristiques peuvent être utilisées ici tant qu’on est plus restrictif que permissif : une marge impossible doit être identifiée comme telle, mais manquer une solution avec une marge extrêmement serrée n’est pas une mauvaise chose.

Mais avec ce changement, une fois qu’une solution est trouvée, il ne suffit plus de concaténer les résultats de simulation pour obtenir la simulation finale. On doit réaliser une simulation complète avec les vraies marges de construction qui évitent tout conflit. Cette étape se rejoint avec celle décrite pour les marges de régularité, qui est maintenant réalisée même sans marge de régularité spécifiée.

6 - Marge de régularité

Une des fonctionnalités qui doit être supportée par STDCM est la marge de régularité. L’utilisateur doit pouvoir indiquer une valeur de marge, exprimée en fonction de la distance ou du temps de parcours, et cette marge doit être ajoutée au trajet.

Par exemple : l’utilisateur peut indiquer une marge de 5 minutes au 100km. Sur un trajet de 42km, un trajet de 10 minutes au plus rapide doit maintenant durer 12 minutes et 6 secondes.

Le problème se situe au niveau de la détection de conflits. En effet, ralentir le train décale l’ensemble du sillon dans le temps et augmente la capacité consommée. La marge doit donc être prise en compte pendant l’exploration pour détecter correctement les conflits.

Pour plus de difficulté, la marge doit suivre le modèle MARECO. La marge n’est pas répartie uniformément sur le trajet, mais selon un calcul qui nécessite de connaître l’ensemble du trajet.

Pendant l’exploration

La principale implication de la marge de régularité est pendant l’exploration du graphe, quand on identifie les conflits. Les temps et les vitesses doivent être baissés linéairement pour prendre en compte les conflits au bon moment. La simulation au plus rapide doit tout de même être calculée car elle peut définir le temp supplémentaire.

Ce procédé n’est pas exact car il ignore la manière dont la marge est appliquée (en particulier pour MARECO). Mais à cette étape les temps exacts ne sont pas nécessaires, il est seulement nécessaire de savoir si une solution existe à ce temps approximatif.

Post-processing

Une fois que le chemin est trouvé, il est nécessaire de faire une simulation finale pour appliquer correctement les marges. Le procédé est le suivant :

1. Pour certains points du chemin, le temps est fixé. C’est un paramètre d’entrée de la simulation qui appelle le module de marge. À l’initialisation, le temps est fixé à chaque point d’arrêt.
2. Une simulation est réalisée. En cas de conflit, on s’intéresse au premier
3. Un point est fixé à la position de ce conflit. Le temps de référence est celui considéré pendant l’exploration.
4. Ce procédé est répété itérativement jusqu’à une absence de conflit

7 - Détails d'implémentation

Cette page précise certains détails d’implémentation. Sa lecture n’est pas nécessaire pour comprendre les principes généraux, mais peut aider avant de se plonger dans le code.

STDCMEdgeBuilder

Cette classe est utilisée pour simplifier la création d’instances de STDCMEdge, les arêtes du graphe. Celles-ci contiennent de nombreux attributs, la plupart pouvant être déterminés en fonction du contexte (comme le nœud précédent). La classe STDCMEdgeBuilder permet de rendre certains attributs optionnels et en calcule d’autres.

Une fois instancié et paramétré, un EdgeBuilder a deux méthodes :

• Collection<STDCMEdge> makeAllEdges() permet de créer toutes les arêtes possibles dans le contexte donné pour une route donnée. S’il y a plusieurs “ouvertures” entre des blocks d’occupation, une arête est créée par ouverture. Tous les conflits, leurs évitements et les attributs associés sont déterminés ici.

• STDCMEdge findEdgeSameNextOccupancy(double timeNextOccupancy) : Cette méthode permet d’obtenir l’arête passant par une certaine “ouverture” (quand elle existe), identifiée ici par le temps de la prochaine occupation sur la route. Elle est utilisée à chaque fois qu’une arête doit être re-créée dans un contexte différent, comme pour appliquer une marge ou corriger une discontinuité. Elle appelle la méthode précédente.

Recherche de chemin

Evaluation des distances

La fonction utilisée pour déterminer la distance (au sens de la recherche de chemin) détermine quel chemin sera privilégié. Le chemin obtenu sera toujours le plus court en fonction du critère donné.

Ici, deux paramètres sont utilisés : le temps de parcours total et l’heure de départ. Le second a un poids très faible par rapport au premier, pour sélectionner en priorité le chemin le plus rapide. Les détails du calcul sont indiqués dans les commentaires des méthodes concernées.

Heuristiques

L’algorithme de recherche de chemin dans le graphe est un A*, avec une heuristique basée sur les coordonnées géographiques.

Cependant, la géométrie des infrastructures générées sont arbitraires, elle ne correspond pas aux distances indiquées sur les voies. Il est donc possible que, sur ces infrastructures, les chemins obtenus ne soient pas les plus courts.

Il est en théorie possible d’utiliser cette heuristique pour déterminer si le chemin en cours d’exploration pourra mener à une solution dont le temps de parcours ne dépasse pas le maximum. Mais pour la même raison, ajouter ce critère rend STDCM inutilisable sur les infrastructures générées. Plus de détails dans cette issue.