Intégration numérique
Introduction
La modélisation physique ayant montré que l’accélération du train était influencée par différents facteurs variant le long du trajet (pente, courbure, force de traction du moteur…), le calcul doit passer par une méthode d’intégration numérique. Le trajet est alors séparé en étapes suffisamment courtes pour considérer tous ces facteurs comme constants, ce qui permet cette fois ci d’utiliser l’équation du mouvement pour calculer le déplacement et la vitesse du train.
La méthode d’intégration numérique d’Euler est la plus simple pour effectuer ce genre de calcul, mais elle présente un certain nombre d’inconvénients. Cet article explique la méthode d’Euler, pourquoi elle ne convient pas aux besoins d’OSRD et quelle méthode d’intégration doit être utilisée à la place.
La méthode d’Euler
La méthode d’Euler appliquée à l’intégration de l’équation du mouvement d’un train est :
$$v(t+dt) = a(v(t), x(t))dt + v(t)$$
$$x(t+dt) = \frac{1}{2}a(v(t), x(t))dt^2 + v(t)dt + x(t)$$
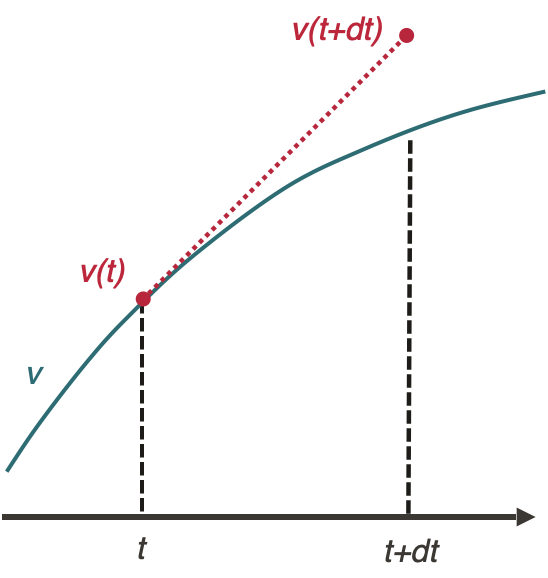
Les avantages de la méthode d’Euler
La méthode d’Euler a pour avantages d’être très simple à implémenter et d’avoir un calcul plutôt rapide pour un pas de temps donné, en comparaison avec d’autres méthodes d’intégration numérique (voir annexe)
Les inconvénients de la méthode d’Euler
La méthode d’intégration d’Euler présente un certain nombre de problèmes pour OSRD :
- Elle est relativement imprécise, et donc nécessite un faible pas de temps, ce qui génère beaucoup de données.
- En intégrant dans le temps, on ne connaît que les conditions du point de départ du pas d’intégration (pente, paramètres d’infrastructure, etc.) car on ne peut pas prédire précisément l’endroit où il se termine.
- On ne peut pas anticiper les futurs changements de directive : le train ne réagit qu’en comparant son état actuel à sa consigne au même instant. Pour illustrer c’est un peu comme si le conducteur était incapable de voir devant lui, alors que dans la réalité il anticipe en fonction des signaux, pentes, virages qu’il voit devant lui.
La méthode Runge-Kutta 4
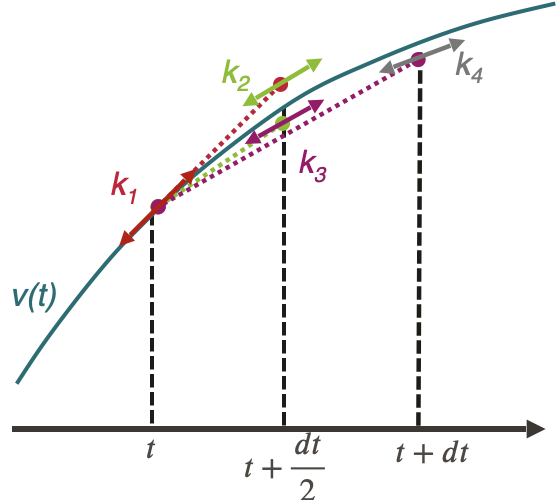
La méthode Runge-Kutta 4 appliquée à l’intégration de l’équation du mouvement d’un train est :
$$v(t+dt) = v(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)dt$$
Avec :
$$k_1 = a(v(t), x(t))$$
$$k_2 = a\Big(v(t+k_1\frac{dt}{2}), x(t) + v(t)\frac{dt}{2} + k_1\frac{dt^2}{8}\Big)$$
$$k_3 = a\Big(v(t+k_2\frac{dt}{2}), x(t) + v(t)\frac{dt}{2} + k_2\frac{dt^2}{8}\Big)$$
$$k_4 = a\Big(v(t+k_3dt), x(t) + v(t)dt + k_3\frac{dt^2}{2}\Big)$$
Les avantages de la méthode de Runge Kutta 4
La méthode d’intégration de Runge Kutta 4 permet de répondre aux différents problèmes soulevés par celle d’Euler :
- Elle permet d’anticiper les changements de directive au sein d’un pas de calcul, représentant ainsi davantage la réalité de conduite d’un train.
- Elle est plus précise pour le même temps de calcul (voir annexe), permettant des étapes d’intégration plus grandes, donc moins de points de données.
Les inconvénients de la méthode de Runge Kutta 4
Le seul inconvénient notable de la méthode de Runge Kutta 4 rencontré pour l’instant est sa difficulté d’implémentation.
Le choix de la méthode d’intégration pour OSRD
Étude de la précision et de la vitesse de calcul
Différentes méthodes d’intégration auraient pu remplacer l’intégration d’Euler de base dans l’algorithme d’OSRD. Afin de décider quelle méthode conviendrait le mieux, une étude sur la précision et la vitesse de calcul de différentes méthodes a été menée. Cette étude sert à comparé les méthodes suivantes :
- Euler
- Euler-Cauchy
- Runge-Kutta 4
- Adams 2
- Adams 3
Toutes les explications sur ces méthodes peuvent être trouvées dans ce document, et le code python utilisé pour la simulation est ici.
La simulation calcule la position et la vitesse d’un TGV accélérant sur une ligne droite plate.
Simulations à pas de temps équivalent
Une courbe de référence a été simulée en utilisant la méthode d’Euler avec un pas de temps de 0,1s, puis le même parcours a été simulé en utilisant les autres méthodes avec un pas de temps de 1s. Il est alors possible de comparer simplement chaque courbe à la courbe de référence, en calculant la valeur absolue de la différence à chaque point calculé. Voici l’erreur absolue résultante de la position du train sur sa distance parcourue :
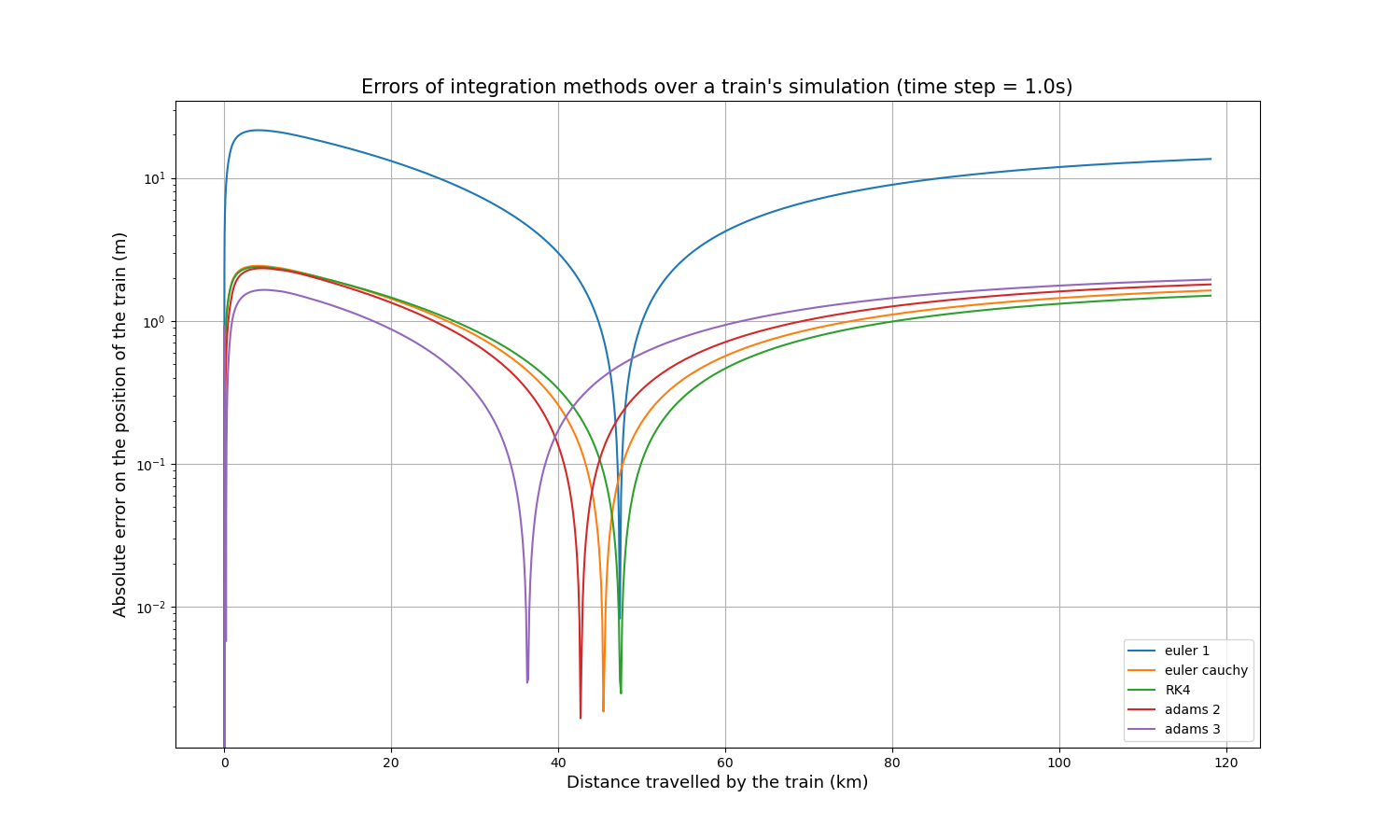
Il apparaît immédiatement que la méthode d’Euler est moins précise que les quatre autres d’environ un ordre de grandeur. Chaque courbe présente un pic où la précision est extrêmement élevée (erreur extrêmement faible), ce qui s’explique par le fait que toutes les courbes commencent légèrement au-dessus de la courbe de référence, la croisent en un point et finissent légèrement en dessous, ou vice versa.
Comme la précision n’est pas le seul indicateur important, le temps de calcul de chaque méthode a été mesuré. Voici ce que nous obtenons pour les mêmes paramètres d’entrée :
| Méthode d’intégration | Temps de calcul (s) |
|---|---|
| Euler | 1.86 |
| Euler-Cauchy | 3.80 |
| Runge-Kutta 4 | 7.01 |
| Adams 2 | 3.43 |
| Adams 3 | 5.27 |
Ainsi, Euler-Cauchy et Adams 2 sont environ deux fois plus lents que Euler, Adams 3 est environ trois fois plus lent, et RK4 est environ quatre fois plus lent. Ces résultats ont été vérifiés sur des simulations beaucoup plus longues, et les différents ratios sont maintenus.
Simulation à temps de calcul équivalent
Comme les temps de calcul de toutes les méthodes dépendent linéairement du pas de temps, il est relativement simple de comparer la précision pour un temps de calcul à peu près identique. En multipliant le pas de temps d’Euler-Cauchy et d’Adams 2 par 2, le pas de temps d’Adams 3 par 3, et le pas de temps de RK4 par 4, voici les courbes d’erreur absolue résultantes :
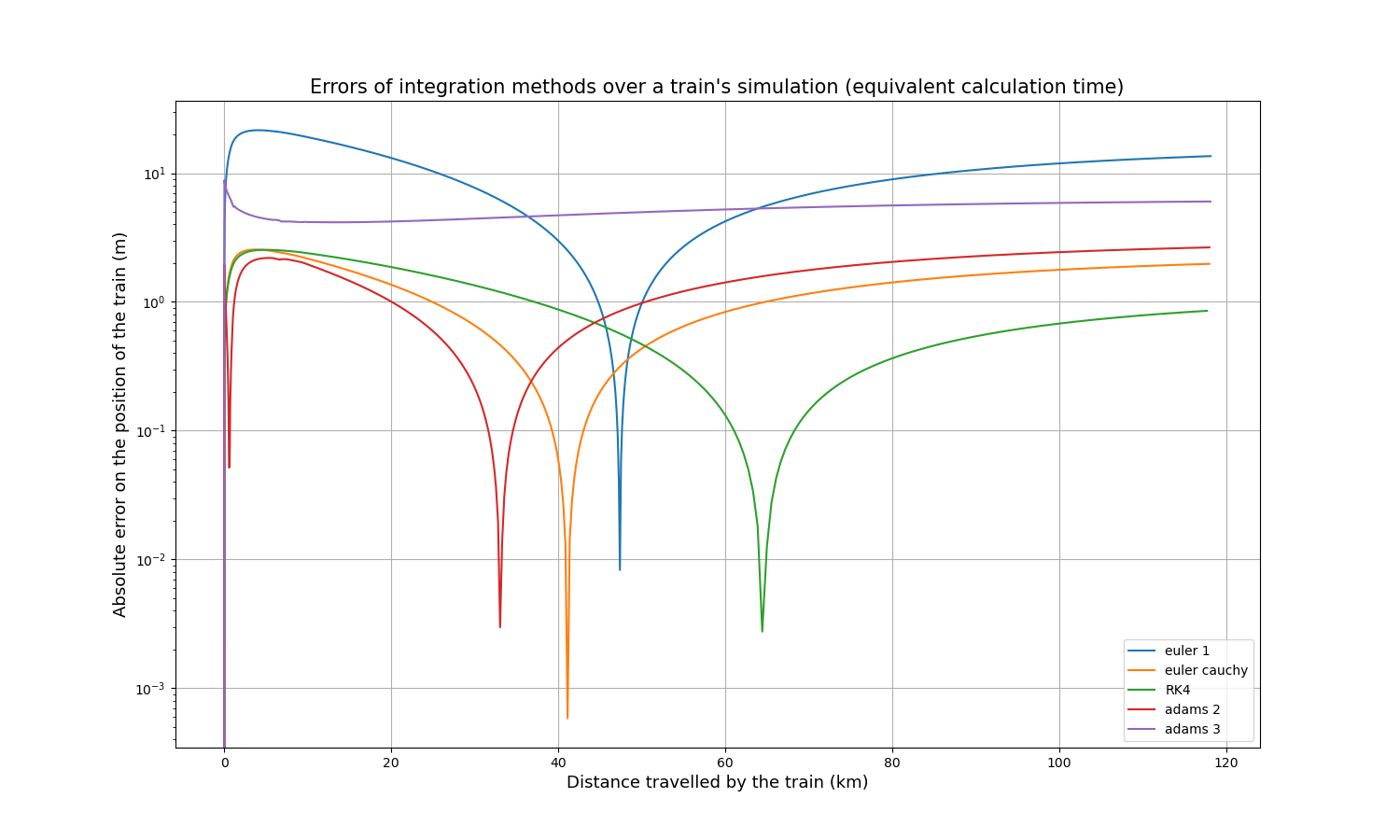
Et voici les temps de calcul :
| Méthode d’intégration | Temps de calcul (s) |
|---|---|
| Euler | 1.75 |
| Euler-Cauchy | 2.10 |
| Runge-Kutta 4 | 1.95 |
| Adams 2 | 1.91 |
| Adams 3 | 1.99 |
Après un certain temps, RK4 tend à être la méthode la plus précise, légèrement plus précise que Euler-Cauchy, et toujours bien plus précise que la méthode d’Euler.
Conclusions de l’étude
L’étude de la précision et de la vitesse de calcul présentée ci-dessus montre que RK4 et Euler-Cauchy seraient de bons candidats pour remplacer l’algorithme d’Euler dans OSRD : les deux sont rapides, précis, et pourraient remplacer la méthode d’Euler sans nécessiter de gros changements d’implémentation car ils ne font que des calculs au sein du pas de temps en cours de calcul. Il a été décidé qu’OSRD utiliserait la méthode Runge-Kutta 4 parce qu’elle est légèrement plus précise que Euler-Cauchy et que c’est une méthode bien connue pour ce type de calcul, donc très adaptée à un simulateur open-source.