Les explications abordent des thèmes et concepts clés d’un point de vue général et fournissent des informations et explications détaillées sur les éléments fondamentaux.
Version imprimable multipages. Cliquer ici pour imprimer.
Explications
- 1: Architecture des conteneurs
- 2: Modèles
- 3: Calcul de marche
- 3.1: Modélisation physique
- 3.2: Intégration numérique
- 3.3: Le système d'enveloppes
- 3.4: Le processus de calcul de marche
- 3.5: Les marges
- 4: Netzgrafik-Editor
1 - Architecture des conteneurs
Il y a 3 principaux conteneurs déployés dans une configuration OSRD standard :
- Gateway (inclut le frontend) : Sert le front-end, gère l’authentification et proxy les requêtes vers le backend.
- Editoast : Agit comme le backend qui interagit avec le front-end.
- Core : Gère les calculs et la logique métier, appelé par Editoast.
Déploiement standard
Le déploiement standard peut être représenté par le diagramme suivant.
flowchart TD
gw["gateway"]
front["fichiers statiques front-end"]
gw -- fichier local --> front
navigateur --> gw
gw -- HTTP --> editoast
editoast -- HTTP --> coreLes requêtes externes sont reçues par le gateway. Si le chemin demandé commence par /api, il sera transféré en utilisant HTTP vers editoast, sinon il servira un fichier avec le chemin demandé. Editoast atteint le core en utilisant HTTP si nécessaire.
Le gateway n’est pas seulement un proxy inverse avec le bundle front-end inclus, il fournit également tous les mécanismes d’authentification : utilisant OIDC ou des tokens.
2 - Modèles
2.1 - Catégories de matériels roulants
Les catégories sont des regroupements de matériel roulant, soit par leurs caractéristiques, leurs performances ou par la nature des dessertes pour lesquelles ils ont été conçus ou sont utilisés.
Un même matériel roulant peut être utilisé pour différents types de circulation, et de desserte. Ce caractère versatile est contenu dans les attributs :
primary_category(requis) indique l’utilisation principale d’un matériel roulantother_categories(optionnel) indique les autres utilisations d’un matériel roulant
La catégorie principale d’un matériel roulant permet plusieurs fonctionnalités, comme le filtrage, un affichage différencié sur les graphiques ou réticulaire, et plus globalement, d’agréger des matériels roulants.
Catégories de matériels roulants
Les différentes catégories de matériel roulant disponibles par défaut sont les suivantes :
Train à grande vitesse(voir High-speed train)Train interurbain(voir Intercity train)Train régional(voir Regional train)Train suburbain(voir Commuter train)Train de fret(voir Freight train)Train de fret rapide(pareil que Train de fret, mais avec un code de composition différent,ME140au lieu deMA100par exemple)Train de nuit(voir Night train)Tram-train(voir Tram-train)Train touristique(voir Touristic train)Train de travaux(voir Work train)
Il est aussi prévu que, plus tard, un utilisateur puisse créer directement de nouvelles catégories de matériel roulant.
Matériels roulants réalistes open data
Afin de rendre l’application plus accessible aux utilisateurs en dehors de l’industrie ferroviaire, tels que des contributeurs externes et des laboratoires de recherche, et de préparer la sortie de la version publique “bac à sable” d’OSRD, plusieurs matériels roulants créés avec des données fictives sont disponibles pour tous les utilisateurs.
Ces matériels roulants ont été conçus pour couvrir la majorité des scénarios de simulation que les utilisateurs pourraient rencontrer.
Ces matériels roulants ne sont pas des matériels roulants existant réellement en raison de la confidentialité des données, mais ils s’en inspirent pour garantir le réalisme des simulations.
Ces matériels roulants sont fournis sous forme de fichiers JSON. Nous avons créé un matériel roulant représentatif de chaque catégorie présentée ci-dessus.
Les caractéristiques de ces matériels roulants ont été calculées à partir des valeurs moyennes des matériels roulants réels de chaque catégorie. De plus, la plupart de ces modèles ont été conçus pour être compatibles avec divers réseaux : ils sont principalement bi-modes (supportant plusieurs tensions et courants d’alimentation), ce qui n’est pas toujours le cas des matériels roulants réels.
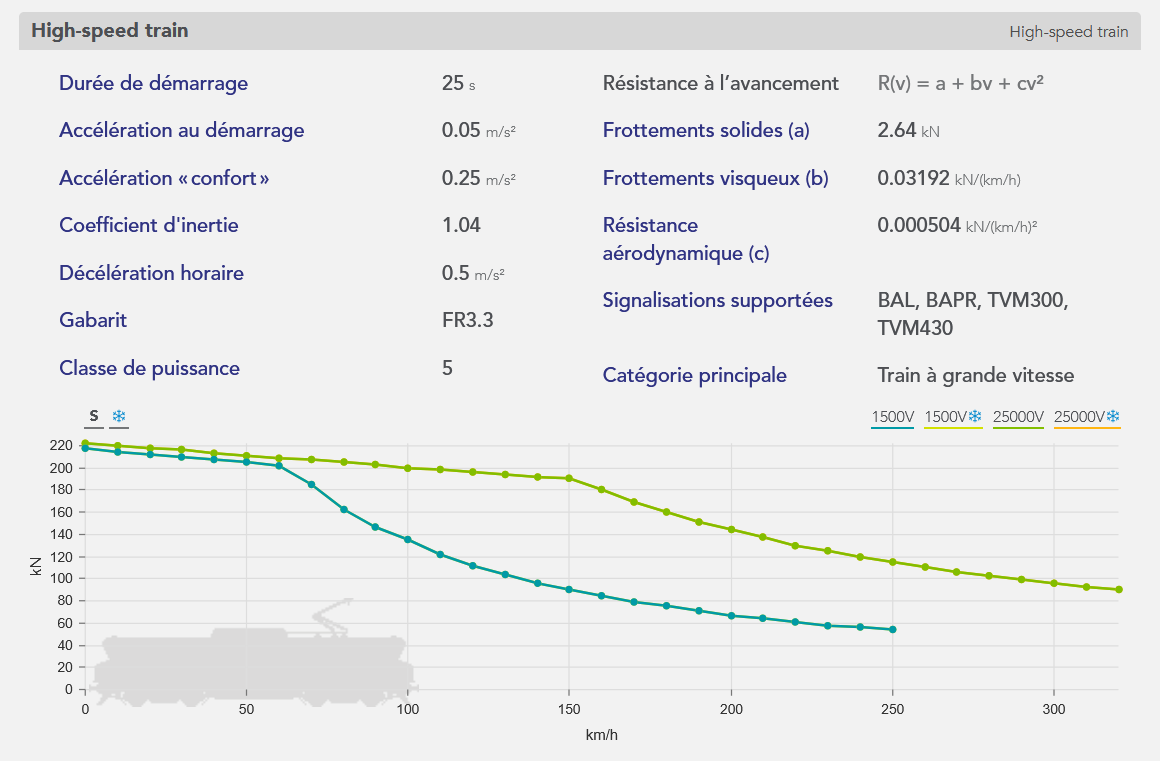
Un exemple de matériel roulant, un train à grande vitesse, est représenté ci-dessous, depuis l’éditeur de matériel roulant de l’application :
Open data
Puisque ces matériels roulants sont fictifs (mais réalistes), ils peuvent être librement utilisés dans des projets en dehors d’OSRD.
Pour y avoir accès et les utiliser dans l’application :
Depuis l’application open-source “bac à sable” : Les matériels roulants sont disponibles par défaut.
Depuis une application lancée localement : Utilisez la commande associée dans le README pour importer les matériels roulants de test dans votre base de données.
./scripts/load-railjson-rolling-stock.sh tests/data/rolling_stocks/realistic/*.json
2.2 - Exemple d'infrastructure
Introduction
Cette page donne un exemple de la manière dont les formats de données sont utilisés pour décrire une infrastructure dans OSRD.
À cette fin, prenons comme exemple l’infrastructure-jouet suivante :
Conseil
Pour zoomer sur un diagramme, cliquez sur le bouton d’édition qui apparaît au survol de celui-ci.Ce diagramme est un aperçu de l’infrastructure avec les lignes et les stations uniquement.
Cette infrastructure ne se veut pas réaliste, mais plutôt destinée à illustrer le modèle de données d’OSRD. Cet exemple sera créé étape par étape et expliqué en cours de route.
Le générateur d’infrastructures
Dans le dépôt OSRD se trouve une bibliothèque python conçue pour aider à générer des infrastructures dans un format compris par OSRD.
L’infrastructure discutée dans cette section peut être générée grâce au fichier small_infra.py. Pour en savoir plus sur les scripts de génération, vous pouvez consulter le README correspondant.
Voies
Sections de voie (Track Sections)
Les premiers objets que nous devons définir sont les TrackSections. La plupart des autres objets sont positionnés par rapport à celles-ci.
Une section de voie est une section de rail (sans aiguillages). On peut choisir de diviser les voies de son infrastructure en autant de sections qu’on le souhaite. Ici, nous avons choisi d’utiliser les sections de voie les plus longues possibles, ce qui signifie qu’entre deux aiguillages, il y a toujours une seule section de voie.
Les sections de voie sont ce sur quoi les trains simulés roulent. Ils sont l’équivalent abstrait des sections de rails physiques. Les sections de voie sont bidirectionnelles.
Dans cet exemple, nous définissons deux voies pour la ligne entre les stations Ouest et Nord-Est. Nous avons également des voies de contournement aux stations Nord et Centre-Ouest pour plus de réalisme. Enfin, nous avons trois voies distinctes dans la station Ouest, puisqu’il s’agit d’une plaque tournante majeure dans notre infrastructure imaginaire.
Important
Les TrackSections sont représentées par des flèches dans ce diagramme pour souligner le fait qu’elles ont un début et une fin. C’est important car les objets positionnés sur les sections de voie sont localisés en fonction de leur distance par rapport au début de leur section de voie.
Par conséquent, pour placer un objet au début de sa section de voie, définissez sa position à 0. Pour le déplacer à la fin de sa section de voie, définissez sa position à la length de la section de voie.
Ces attributs sont nécessaires pour que la section de voie soit complète :
length: la longueur de la section de voie en mètres.geo: les coordonnées dans la réalité (geo pour géographique), au format GeoJSON.- attributs cosmétiques :
line_name,track_name,track_numberqui sont utilisés pour indiquer le nom et les étiquettes qui ont été donnés aux voies / lignes dans la réalité.
Pour toutes les sections de voies de notre infrastructure, les attributs geo se rapprochent beaucoup au schéma donné.
Pour la plupart des sections de voies, leur length est proportionnelle à ce que l’on peut voir sur le diagramme. Pour préserver la lisibilité, des exceptions ont été faites pour TA6, TA7, TD0 et TD1 (qui font 10km et 25km).
Nœud
Un Node représente un nœud dans l’infrastructure. Dans une simulation OSRD, un train ne peut passer d’une section de voie à une autre que si elles sont reliées par un nœud.
Un nœud peut se présenter de deux manières différentes :
1) Aiguillages
Les aiguillages peuvent être vus comme une collection de liens de sections de voies, partitionnés en groupes. Chaque groupe représente un état de l’aiguillage. Passer d’un groupe à un autre peut prendre du temps, et au maximum un lien peut être prêt à être utilisé à la fois.
Dans le monde réel, les aiguillages ne sont pas uniques, mais plutôt des instances de modèles existants.
2) Liens de sections de voies
Pour le moment, nous n’avons créé que des sections de voies, qui ne sont pas interconnectées (les données géospatiales ne sont pas utilisées pour déduire quelles voies sont connectées).
Les link sont utilisés pour connecter deux sections de voie ensemble, tout comme un joint de soudure le ferait dans la vie réelle. Dans une simulation OSRD, un train ne peut passer d’une section de voie à une autre que si elles sont reliées par ce type de nœud, le link (ou par un autre NodeType).
Que ce soit pour les aiguillages ou les liens de sections de voies, les liens et les groupes ne font pas partie du switch lui-même, mais d’un objet NodeType, qui est partagé par les aiguillages du même modèle.
Types de Nœud
Les NodeTypes ont deux attributs obligatoires :
ports: Une liste de noms de ports. Un port est une extrémité du nœud qui peut être connecté à une section de voie.groups: Un table de correspondance entre le nom des groupes et les listes de branches (connexion entre 2 ports) qui caractérisent les différentes positions possibles du type de nœud
À tout moment, tous les nœuds ont un groupe actif, et peuvent avoir une branche active, qui appartient toujours au groupe actif. Pendant une simulation, le changement de branche active à l’intérieur d’un groupe est instantané, mais le changement de branche active entre les groupes prend un temps configurable.
Ceci est dû au fait qu’un Nœud peut-être un objet physique (dans le cas des aiguillages), et que le changement de branche active peut impliquer le déplacement de certaines de ses parties. Les groups sont conçus pour représenter les différentes positions qu’un Nœud peut avoir. Chaque groupe contient les liens qui peuvent être utilisés dans la position du Nœud associé.
Dans le cas des aiguilles, la durée nécessaire pour changer de groupe est stockée à l’intérieur du Nœud, car elle peut varier en fonction de l’implémentation physique du modèle d’aiguillage.
Nos exemples utilisent actuellement cinq NodeTypes. Il est possible d’ajouter un type de nœud si nécessaire via le champ extended_node_type.
1) Le lien entre deux sections de voies
Celui-ci représente le lien entre deux sections de voies. Il possède deux ports : A et B.
Il permet de créer un lien entre deux sections de voies tel que définis dans OSRD. Ce n’est pas un objet physique.
2) L’aiguille
L’omniprésent aiguillage en Y, qui peut être considéré comme la fusion de deux voies ou la séparation d’une voie.
Ce type d’aiguillage possède trois ports : A, B1 et B2.
Il y a deux groupes, chacun avec une connexion dans leur liste : A_B1, qui connecte A à B1, et A_B2 qui connecte A à B2.
Ainsi, à tout moment (sauf lorsque l’aiguille bouge pour changer de groupe), un train peut aller de A à B1 ou de A à B2 mais jamais aux deux en même temps. Un train ne peut pas aller de B1 à B2.
Une aiguille n’a que deux positions :
- A vers B1
- A vers B2
3) L’aiguillage de croisement
Il s’agit simplement de deux voies qui se croisent.
Ce type a quatre ports : A1, B1, A2 et B2.
Il ne comporte qu’un seul groupe contenant deux connexions : A1 vers B1 et A2 vers B2. En effet, ce type d’aiguillage est passif : il n’a pas de pièces mobiles. Bien qu’il n’ait qu’un seul groupe, il est tout de même utilisé par la simulation pour faire respecter les réservations de route.
Voici les deux connexions différentes que ce type d’aiguillage possède :
- A1 vers B1
- A2 vers B2
4) L’aiguillage de croisement double
Celui-ci ressemble plus à deux aiguilles dos à dos. Il possède quatre ports : A1, A2, B1 et B2.
Cependant, il comporte quatre groupes, chacun avec une connexion. Les quatre connexions possibles sont les suivantes :
- A1 vers B1
- A1 vers B2
- A2 vers B1
- A2 vers B2
5) L’aiguillage de croisement simple
Celui-ci ressemble plus à un mélange entre une aiguille simple et un croisement. Il possède quatre ports : A1, A2, B1 et B2.
Voici les trois connexions que peut réaliser cet aiguillage :
- A1 vers B1
- A1 vers B2
- A2 vers B2
Retour aux nœuds
Un Node possède trois attributs :
node_type: l’identifiantNodeTypede ce nœud.ports: une correspondance entre les noms de port et les extrémités des sections de voie.group_change_delay: le temps qu’il faut pour changer le groupe de l’aiguillage qui est actif.
Les noms des ports doivent correspondre aux ports du type du nœud choisi. Les extrémités de la section de voie peuvent être début ou fin, faites attention à choisir les bonnes.
La plupart des nœuds de notre exemple sont des nœuds habituels. Le chemin de la gare du Nord à la gare du Sud a deux aiguillages de croisement. Enfin, il y a un aiguillage de croisement double juste avant que la ligne principale ne se divise en lignes Nord-Est et Sud-Est.
Il est important de noter que ces nœuds sont présents par défaut dans le code du projet. Seuls les extended_switch_type ajoutés par l’utilisateur apparaîtront dans le railjson.
Courbes et pentes
Les Courbes et les Pentes sont essentielles pour des simulations réalistes. Ces objets sont définis comme une plage entre une position de début (begin) et de fin (end) sur une section de voie. Si une courbe / pente s’étend sur plus d’une section de voie, elle doit être ajoutée à toutes les sections.
Les valeurs des courbes / pentes sont constantes sur toute leur étendue. Pour des courbes / pentes variables, il faut créer plusieurs objets.
Les valeurs de pente sont mesurées en mètres par kilomètres, et les valeurs de courbe sont mesurées en mètres (le rayon de la courbe).
begin doit toujours être inférieure à la valeur end. C’est pourquoi les valeurs de courbe/pente peuvent être négatives : une pente ascendante de 1 allant du décalage 10 à 0 est identique à une pente descendante de -1 allant des décalages 0 à 10.Dans le fichier small_infra.py, nous avons des pentes sur les sections de voie TA6, TA7, TD0 et TD1.
Il y a également des courbes sur les sections de voie TE0, TE1, TE3 et TF1.
Enclenchement
Jusqu’à présent, tous les objets ont contribué à la topologie (forme) des voies. La topologie serait suffisante pour que les trains puissent naviguer sur le réseau, mais pas assez pour le faire en toute sécurité. pour assurer la sécurité, deux systèmes collaborent :
- L’enclenchement garantit que les trains sont autorisés à avancer
- La signalisation est le moyen par lequel l’enclenchement communique avec le train
Détecteurs
Ces objets sont utilisés pour créer des sections TVD (Track Vacancy Detection) : la zone de la voie située entre deux détecteurs est une section TVD. Lorsqu’un train rencontre un détecteur, la section dans laquelle il entre est occupée. La seule fonction des sections TVD est de localiser les trains.
Dans la réalité, les détecteurs peuvent être des compteurs d’essieux ou des circuits de voie par exemple.
Pour que cette méthode de localisation soit efficace, les détecteurs doivent être placés régulièrement le long de vos voies, pas trop nombreux pour des raisons de coût, mais pas trop peu, car les sections TVD seraient alors très grandes et les trains devraient être très éloignés les uns des autres pour être distingués, ce qui réduirait la capacité.
Il y a souvent des détecteurs à proximité de tous les extrémités des aiguillages. De cette façon, l’enclenchement est averti presque immédiatement lorsqu’un aiguillage est libéré, qui est alors libre d’être utilisé à nouveau.
Dans OSRD, les détecteurs sont des objets ponctuels. Les attributs dont ils ont besoin sont leur id et leur localisation sur la voie (track et offset).
Quelques notes :
- Entre certains points, nous n’avons ajouté qu’un seul détecteur (et non pas deux), car ils étaient très proches les uns des autres, et cela n’aurait eu aucun sens de créer une minuscule section TVD entre eux. Cette situation s’est produite sur des sections de voies (TA3, TA4, TA5, TF0 et TG3).
- Dans notre infrastructure, il y a relativement peu de sections de voie qui sont assez longues pour nécessiter plus de détecteurs que ceux liés aux aiguillages. Ce sont, TA6, TA7, TDO, TD1, TF1, TG1 et TH1. Par exemple, TD0, qui mesure 25 km, compte en fait 17 détecteurs au total.
Butoirs (BufferStops)
Les BufferStops sont des obstacles destinés à empêcher les trains de dérailler en bout des voies.
Dans notre infrastructure, il y a un butoir sur chaque section de voie qui est un cul-de-sac. Il y a donc 8 butoirs au total.
Avec les détecteurs, ils définissent les limites des sections TVD (voir Détecteurs).
Itinéraires (Routes)
Une Route est un itinéraire dans l’infrastructure. Un sillon est une séquence de routes. Les itinéraires sont utilisés pour réserver des sections de sillon avec l’enclenchement. Voir la documentation dédiée.
Il est représenté avec les attributs suivants :
entry_pointetexit_point: Références de détecteurs ou de butées qui marquent le début et la fin de l’itinéraire.entry_point_direction: Direction à prendre sur la section de voie depuisentry_pointpour commencer l’itinéraire.switches_direction: Un ensemble de directions à suivre lorsqu’on rencontre un aiguillage sur notre itinéraire, de manière à reconstituer cet itinéraire deentry_pointjusqu’àexit_point.release_detectors: Lorsqu’un train franchit un détecteur de libération, les ressources réservées depuis le début de la route jusqu’à ce détecteur sont libérées.
Signalisation
Grâce à l’enclenchement, les trains sont localisés et autorisés à se déplacer. C’est un bon début, mais c’est inutile tant que les trains n’en sont pas informés. C’est là que les “signaux” entrent en jeu : les signaux réagissent aux enclenchements et peuvent être vus par les trains.
La façon dont les trains réagissent aux signaux dépend de l’aspect, du type de signal et du système de signalisation.
Voici les attributs les plus importants des signaux :
linked_detector: Le détecteur lié.type_code: Le type de signal.direction: La direction qu’il protège, qui peut être simplement interprétée comme la façon dont il peut être vu par un train entrant (puisqu’il n’y a des feux que d’un côté…). La direction est relative à l’orientation de la section de voie.- Des attributs cosmétiques comme
angle_geoandsidequi contrôlent la manière dont les signaux sont affichés dans le front-end.
Voici une visualisation de comment on peut représenter un signal, et quelle direction il protège.
La manière dont les signaux sont disposés dépend fortement du système de signalisation et du gestionnaire de l’infrastructure.
Voici les règles de base utilisées pour cet exemple d’infrastructure :
- Nous ajoutons deux signaux d’espacement (un par direction) pour chaque détecteur qui découpe une longue section de TVD en plus petites sections.
- Les entrées d’aiguillage où un train pourrait devoir s’arrêter sont protégées par un signal (qui est situé à l’extérieur de la section TVD de l’aiguillage). Il doit être visible depuis la direction utilisée pour approcher l’aiguillage. Lorsqu’il y a plusieurs aiguillages dans une rangée, seul le premier a généralement besoin d’être protégé, car l’enclenchement est généralement conçu pour ne pas encourager les trains à s’arrêter au milieu des intersections.
Notez que les détecteurs liés à au moins un signal ne sont pas représentés, car il n’y a pas de signaux sans détecteurs associés dans cet exemple.
Pour obtenir le id d’un détecteur lié à un signal, prenez le id du signal et remplacez S par D (par exemple SA0 -> DA0).
Électrification
Pour permettre à des trains électriques de circuler sur notre infrastructure, nous devons spécifier les parties de celle-ci qui sont électrifiées.
Caténaires (Catenaries)
Les Catenaries représentent les câbles d’alimentation qui alimentent les trains électriques. Ils sont représentés avec les attributs suivants :
voltage: Une chaîne de caractères représentant le type d’alimentation électrique utilisée pour l’électrification.track_ranges: Une liste de portions de sections de voie (TrackRanges) couvertes par cette caténaire. UneTrackRangeest composée d’un identifiant de section de voie, d’une positionbeginet d’une positionend.
Dans notre exemple, nous avons deux Catenaries:
- Une avec
voltagedéfini sur"1500", qui couvre uniquement TA0. - Une avec
voltagedéfini sur"25000", qui couvre tous les autres sauf TD1.
Cela signifie que seuls les trains thermiques peuvent traverser la section de voie TD1.
Notre exemple montre également que, contrairement à son homologue réel, une seule Catenary peut couvrir toute l’infrastructure.
Sections Neutres (NeutralSections)
Dans certaines parties d’une infrastructure, les conducteurs de train sont sommés - principalement pour des raisons de sécurité - de couper l’alimentation électrique du train.
Pour représenter de telles parties, nous utilisons des NeutralSections. Elles sont représentées avec principalement les attributs suivants :
track_ranges: Une liste deDirectedTrackRanges(portions de sections de voie associées à une direction) couvertes par cette section neutre.lower_pantograph: Un booléen indiquant si le pantographe du train doit être abaissé pendant la traversée de cette section.
Dans notre exemple, nous avons trois NeutralSections : une à la jonction des caténaires "1500" et "25000", une sur TA6 et une sur TG1 et TG4.
Pour plus de détails sur le modèle, voir la page dédiée.
Divers
Points opérationnels (OperationalPoints)
Le point opérationnel est aussi connu sous le nom de Point Remarquable (PR).
Un OperationalPoint est une collection de points (OperationalPointParts) d’intérêt.
Par exemple, il peut être pratique (repère de conduite) de stocker l’emplacement des plateformes en tant que parties et de les regrouper par station dans des points opérationnels.
De la même manière, un pont au-dessus des voies sera un OperationalPoint, mais il comportera plusieurs OperationPointParts, une à l’intersection de chaque voie. Le champ local_track_name fournit un label lisible pour la voie dans le contexte d’un point opérationnel.
Dans l’exemple de l’infrastructure, nous n’avons utilisé que des points opérationnels pour représenter les stations. Les parties de points opérationnels sont représentées par des diamants violets. Gardez à l’esprit qu’un seul point opérationnel peut contenir plusieurs parties.
Limites de gabarit (Loading Gauge Limits)
Cet objet s’apparente aux Pentes et aux Courbes : il couvre une plage de section de voie, avec une position de début (begin) et de fin (end). Il représente une restriction sur les trains qui peuvent circuler sur la plage donnée, par poids ou par type de train (fret ou passagers).
Nous n’en avons pas mis dans nos exemples.
Sections de vitesse (SpeedSections)
Les SpeedSections représentent les limites de vitesse (en mètres par seconde) qui sont appliquées sur certaines parties des voies. Une SpeedSection peut s’étendre sur plusieurs sections de voie, et ne couvre pas nécessairement la totalité des sections de voie. Les sections de vitesse peuvent se chevaucher.
Dans notre exemple d’infrastructure, nous avons une section de vitesse couvrant l’ensemble de l’infrastructure, limitant la vitesse à 300 km/h. Sur une plus petite partie de l’infrastructure, nous avons appliqué des sections de vitesse plus restrictives.
2.3 - Zones neutres
Objet physique que l’on cherche à modéliser
Introduction
Pour qu’un train puisse circuler, il faut soit qu’il ait une source d’énergie à bord (fuel, batterie, hydrogène, …) soit qu’on l’alimente en énergie tout au long de son parcours.
Pour fournir cette énergie, des câbles électriques sont suspendus au dessus des voies: les caténaires. Le train assure ensuite un contact avec ces câbles grâce à un patin conducteur monté sur un bras mécanique: le pantographe.
Zones neutres
Avec ce système il est difficile d’assurer l’alimentation électrique d’un train en continu sur toute la longueur d’une ligne: sur certaines portions de voie, il est nécessaire de couper l’alimentation électrique du train. Ce sont ces portions que l’on appelle zones neutres.
En effet, pour éviter les pertes énergétiques le long des caténaires, le courant est fourni par plusieurs sous-stations réparties le long des voies. Deux portions de caténaires alimentées par des sous-stations différentes doivent être isolées électriquement pour éviter les courts-circuits.
Par ailleurs, la façon dont les voies sont électrifiées (courant continu ou non par exemple) peut changer selon les us locaux et l’époque d’installation. Il faut également isoler électriquement les portions de voies qui sont électrifiées différemment. Le train doit aussi (sauf cas particuliers) changer de pantographe lorsqu’il change de type d’électrification.
Dans ces deux cas on indique alors au conducteur de couper la traction du train, et parfois même d’en baisser le pantographe.
Dans l’infrastructure française, ces zones sont signalées par des panneaux d’annonce, d’exécution et de fin. Ces panneaux portent par ailleurs l’indication de baisser le pantographe ou non. Les portions de voies entre l’exécution et la fin peuvent ne pas être électrifiées entièrement, et même ne pas posséder de caténaire (dans ce cas la zone nécessite forcément de baisser le pantographe).
Parfois, des pancartes REV (pour réversible) sont placées en aval des panneaux de fin de zone. Elles sont destinées aux trains qui circulent avec un pantographe à l’arrière du train. Ces pancartes indiquent que le conducteur peut reprendre la traction en toute sécurité.
Par ailleurs il peut parfois être impossible sur une courte portion de voie de placer une caténaire ou bien de lever le pantographe du train. Dans ce cas la ligne est tout de même considérée électrifiée, et la zone sans électrification (passage sous un pont par exemple) est considérée comme une zone neutre.
Matériel roulant
Après avoir traversé une zone neutre, un train doit reprendre la traction. Ce n’est pas immédiat (quelques secondes), et la durée nécessaire dépend du matériel roulant.
Il doit également, le cas échéant, relever son pantographe, ce qui prend également du temps (quelques dizaines de secondes) et dépend également du matériel roulant.
Ainsi la marche sur l’erre imposée au train s’étend en dehors de la zone neutre, puisque ces temps systèmes sont à décompter à partir de la fin de la zone neutre.
Modèle de données
Nous avons choisi de modéliser les zones neutres comme l’espace entre les panneaux liés à celle-ci (et non pas comme la zone précise où il n’y a pas de caténaire ou bien où la caténaire n’est pas électrifiée).
Cette zone est directionnelle, i.e. associée à un sens de circulation, pour pouvoir prendre en compte des placements de panneaux différents selon le sens. Le panneau d’exécution d’un sens donné n’est pas nécessairement placé à la même position que le panneau de fin de zone du sens opposé.
Pour une voie à double sens, une zone neutre est donc représentée par deux objets.
Le schema est le suivant
{
"lower_pantograph": boolean,
"track_ranges": [
{
"track": string,
"start": number,
"end": number,
"direction": enum
}
],
"announcement_track_ranges": [
{
"track": string,
"start": number,
"end": number,
"direction": enum
}
]
}
lower_pantograph: indique si le pantographe doit être baissé dans cette zonetrack_ranges: liste des portions de voie où le train ne doit pas tractionnerannouncement_track_ranges: liste des portions de voie entre le panneau d’annonce et le panneau d’exécution
Affichage
Cartographie
Les zones affichées dans la cartographie correspondent aux track_ranges, donc entre les panneaux d’exécution et de fin de zone. La couleur de la zone indique si le train doit baisser son pantographe dans la zone ou non.
La direction dans laquelle la zone s’applique n’est pas représentée.
Résultat de simulation
Dans l’affichage linéaire, c’est toujours la zone entre EXE et FIN qui est affichée.
Recherche d’itinéraire
Les zones neutres sont donc des portions de voie “non électrifiées” où un train électrique peut tout de même circuler (mais où il ne peut pas tractionner).
Lors de la recherche de chemin dans l’infrastructure, une portion de voie qui n’est pas couverte par les track_ranges d’un objet caténaire (documentation à écrire) peut être empruntée par un train électrique seulement si elle est couverte par les track_ranges d’une zone neutre.
Simulation
Dans la simulation, nous approximons le comportement du conducteur de la façon suivante :
- La marche sur l’erre est entamée dès que la tête du train passe le panneau d’annonce
- Le décompte des temps systèmes (relevé du pantographe et reprise de la traction) commence dès que la tête du train passe le panneau de fin.
Dans la simulation actuelle, il est plus facile de manier des bornes d’intégration spatiales que temporelles. Nous effectuons l’approximation suivante: lors de la sortie de la zone neutre, on multiplie les temps systèmes par la vitesse en sortie de zone. La marche sur l’erre est alors prolongée de la distance obtenue. Cette approximation est raisonnable car l’inertie du train et la quasi-absence de frottement garantissent que la vitesse varie peu sur cet intervalle de temps.
Potentielles améliorations
Plusieurs points pourraient être améliorés :
- On ne considère pas les pancartes REV, tous les trains ne possèdent donc qu’un pantographe à l’avant dans nos simulations.
- Les temps systèmes sont approximés.
- Le comportement conducteur est plutôt restrictif (la marche sur l’erre pourrait commencer après le panneau d’annonce).
- L’affichage des zones est limité: pas de représentation de la direction ou des zones d’annonce.
- Ces zones ne sont pas éditables.
3 - Calcul de marche
OSRD peut être utilisé pour effectuer deux types de calculs :
- Calcul de marche (standalone train simulation) : calcul du temps de parcours d’un train sur un trajet donné, effectué sans interaction entre le train et le système de signalisation.
- Simulation : calcul “dynamique” de plusieurs trains interagissant entre eux via le système de signalisation.
1 - Les données d’entrée
Un calcul de marche est basé sur 5 entrées :
- L’infrastructure : Topologie des lignes et des voies, position des gares et bâtiments voyageurs, position et type des aiguilles, signaux, vitesses maximales de ligne, profil de ligne corrigée (pentes, rampes et virages).
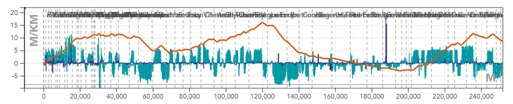
L’histogramme bleu est une représentation des déclivités en [‰] par position en [m]. Les déclivités sont positives pour les rampes et négatives pour les pentes.
La ligne orange représente le profil cumulé, c’est-à-dire l’altitude relative par rapport au point de départ.
La ligne bleue est une représentation des virages en termes de rayons des courbures en [m].
- Le matériel roulant : Dont les caractéristiques nécessaires pour effectuer la simulation sont représentées ci-dessous.

La courbe orange, appelée courbe effort-vitesse du matériel, représente l’effort moteur maximal en fonction de la vitesse de circulation.
La longueur, la masse, et la vitesse max du train sont représentées en bas de l’encadré.
L’horaire de départ permettant ensuite de calculer les horaires de passage aux différents points remarquables (dont gares).
Les marges : Temps ajouté au trajet du train pour détendre sa marche (voir page sur les marges).
- Le pas de temps pour le calcul de l’intégration numérique.
2 - Les résultats
Les résultats d’un calcul de marche peuvent se représenter sous différentes formes :
- Le graphique espace/temps (GET) : représente le parcours des trains dans l’espace et dans le temps, sous la forme de traits globalement diagonaux dont la pente est la vitesse. Les arrêts apparaissent sous la forme de plateaux horizontaux.
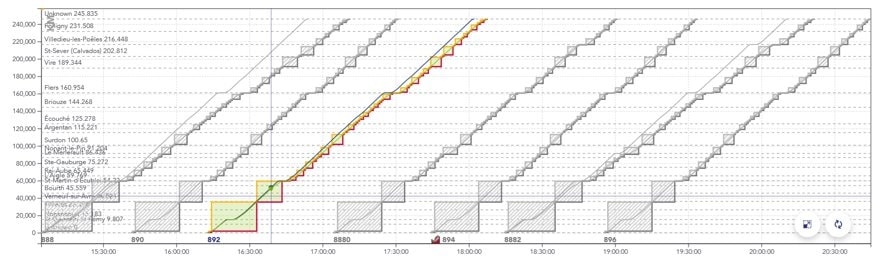
Exemple de GET avec plusieurs trains espacés d’environ 30mn.
L’axe x est l’horaire de passage du train, l’axe y est la position du train en [m].
La ligne bleue représente le calcul de marche le plus tendu pour le train, la ligne verte représente un calcul de marche détendu, dit « économique ».
Les rectangles pleins entourant les trajets représentent les portions de la voie successivement réservées au passage du train (appelées cantons).
- Le graphique espace/vitesse (GEV) : représente le parcours d’un seul train, cette fois-ci en termes de vitesse. Les arrêts apparaissent donc sous forme de décrochages de la courbe jusqu’à zéro, suivis d’un ré-accélération.

L’axe x est la position du train en [m], l’axe y est la vitesse du train en [km/h] .
La ligne violette représente la vitesse maximale autorisée.
La ligne bleue représente la vitesse dans le cas du calcul de marche le plus tendu.
La ligne verte représente la vitesse dans le cas du calcul de marche « économique ».
- Les horaires de passage du train aux différents points remarquables
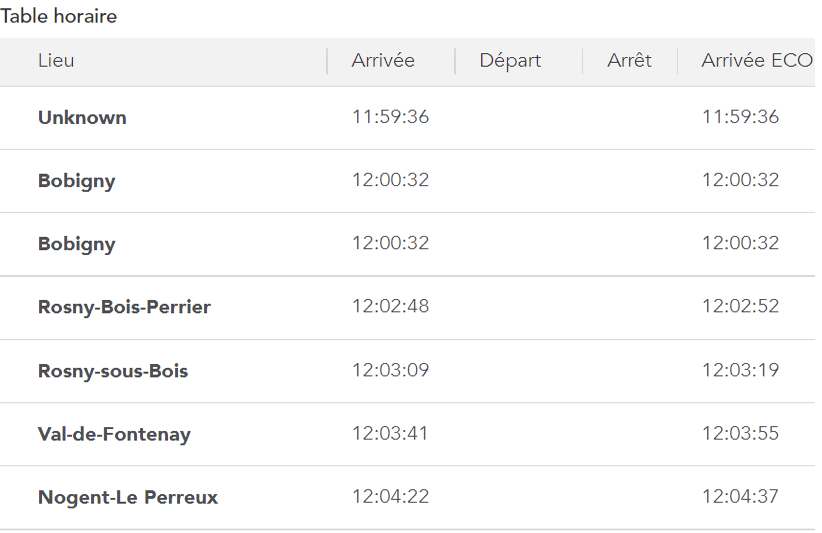
3.1 - Modélisation physique
La modélisation physique joue un rôle important dans le cœur de calcul d’OSRD. C’est elle qui nous permet de simuler la circulation des trains, et elle doit être aussi réaliste que possible.
Bilan des forces
Pour calculer le déplacement du train au cours du temps, il faut d’abord calculer sa vitesse à chaque instant. Une manière simple d’obtenir cette vitesse est de passer par le calcul de l’accélération. Grâce au principe fondamental de la dynamique, l’accélération du train à chaque instant est directement dépendant des différentes forces qui lui sont appliquées : $$ \sum \vec{F}=m\vec{a} $$

Traction : La valeur de la force de traction \(F_{mot}\) dépend de plusieurs facteurs :
- du matériel roulant
- de la vitesse du train \(v^{\prime}x\), selon la courbe effort-vitesse ci-dessous :
$$ {\vec{F_{mot}}(v_{x^{\prime}}, x^{\prime})=F_{mot}(v_{x^{\prime}}, x^{\prime})\vec{e_x^{\prime}}} $$

L’axe x représente la vitesse du train en [km/h], l’axe y, la valeur de la force de traction en [kN].
- de l’action du conducteur, qui accélère plus ou moins fort en fonction de l’endroit où il se trouve sur son trajet
- Freinage : La valeur de la force de freinage \(F_{brk}\) dépend elle aussi du matériel roulant et de l’action du conducteur mais possède une valeur constante pour un matériel donné. Dans l’état actuel de la modélisation, le freinage est soit nul, soit à sa valeur maximale.
$$ \vec{F_{brk}}(x^{\prime})=-F_{brk}(x^{\prime}){\vec{e_{x^{\prime}}}} $$
Une seconde approche de la modélisation du freinage est l’approche dite horaire, car utilisée pour la production horaire à la SNCF. Dans ce cas, la décélération est fixe et le freinage ne dépend plus des différentes forces appliquées au train. Les valeurs de décélération typiques vont de 0.4 à 0.7m/s².
- Résistance à l’avancement : Pour modéliser la résistance à l’avancement du train on utilise la formule de Davis qui prend en compte tous les frottements et la résistance aérodynamique de l’air. La valeur de la résistance à l’avancement dépend de la vitesse \(v^{\prime}_x\). Les coefficients \(A\), \(B\), et \(C\) dépendent du matériel roulant.
$$ {\vec{R}(v_{x^{\prime}})}=-(A+Bv_{x^{\prime}}+{Cv_{x^{\prime}}}^2){\vec{e_{x^{\prime}}}} $$
- Poids (pentes + virages) : La force du poids donnée par le produit entre la masse \(m\) du train et la constante gravitationnelle \(g\) est projetée sur les axes \(\vec{e_x}^{\prime}\) et \(\vec{e_y}^{\prime}\).Pour la projection, on utilise l’angle \(i(x^{\prime})\), qui est calculé à partir de l’angle de déclivité \(s(x^{\prime})\) corrigé par un facteur qui prend en compte l’effet du rayon de virage \(r(x^{\prime})\).
$$ \vec{P(x^{\prime})}=-mg\vec{e_y}(x^{\prime})= -mg\Big[sin\big(i(x^{\prime})\big){\vec{e_{x^{\prime}}}(x^{\prime})}+cos\big(i(x^{\prime})\big){\vec{e_{{\prime}}}(x^{\prime})}\Big] $$
$$ i(x^{\prime})= s(x^{\prime})+\frac{800m}{r(x^{\prime})} $$
- Réaction du sol : La force de réaction du sol compense simplement la composante verticale du poids, mais n’a pas d’impact sur la dynamique du train car elle n’a aucune composante selon l’axe \({\vec{e_x}^{\prime}}\).
$$ \vec{R_{gnd}}=R_{gnd}{\vec{e_{y^{\prime}}}} $$
Equilibre des forces
L’équation du principe fondamental de la dynamique projetée sur l’axe \({\vec{e_x}^{\prime}}\) (dans le référentiel du train) donne l’équation scalaire suivante :
$$ a_{x^{\prime}}(t) = \frac{1}{m}\Big [F_{mot}(v_{x^{\prime}}, x^{\prime})-F_{brk}(x^{\prime})-(A+Bv_{x^{\prime}}+{Cv_{x^{\prime}}}^2)-mgsin(i(x^{\prime}))\Big] $$
Celle-ci est ensuite simplifiée en considérant que malgré la pente le train se déplace sur un plan et en amalgamant \(\vec{e_x}\) et \(\vec{e_x}^{\prime}\). La pente a toujours un impact sur le bilan des forces mais on considère que le train ne se déplace qu’horizontalement, ce qui donne l’équation simplifiée suivante :
$$ a_{x}(t) = \frac{1}{m}\Big[F_{mot}(v_{x}, x)-F_{brk}(x)-(A+Bv_{x}+{Cv_{x}}^2)-mgsin(i(x))\Big] $$
Résolution
La force motrice et la force de freinage dépendent de l’action du conducteur (il décide d’accélérer ou de freiner plus ou moins fort en fonction de la situation). Cette dépendance se traduit donc par une dépendance de ces deux forces à la position du train. La composante du poids dépend elle aussi de la position du train, car provenant directement des pentes et des virages situées sous ce dernier.
De plus, la force motrice dépend de la vitesse du train (selon la courbe effort vitesse) tout comme la résistance à l’avancement.
Ces différentes dépendances rendent impossible la résolution analytique de cette équation, et l’accélération du train à chaque instant doit être calculée par intégration numérique.
3.2 - Intégration numérique
Introduction
La modélisation physique ayant montré que l’accélération du train était influencée par différents facteurs variant le long du trajet (pente, courbure, force de traction du moteur…), le calcul doit passer par une méthode d’intégration numérique. Le trajet est alors séparé en étapes suffisamment courtes pour considérer tous ces facteurs comme constants, ce qui permet cette fois ci d’utiliser l’équation du mouvement pour calculer le déplacement et la vitesse du train.
La méthode d’intégration numérique d’Euler est la plus simple pour effectuer ce genre de calcul, mais elle présente un certain nombre d’inconvénients. Cet article explique la méthode d’Euler, pourquoi elle ne convient pas aux besoins d’OSRD et quelle méthode d’intégration doit être utilisée à la place.
La méthode d’Euler
La méthode d’Euler appliquée à l’intégration de l’équation du mouvement d’un train est :
$$v(t+dt) = a(v(t), x(t))dt + v(t)$$
$$x(t+dt) = \frac{1}{2}a(v(t), x(t))dt^2 + v(t)dt + x(t)$$

Les avantages de la méthode d’Euler
La méthode d’Euler a pour avantages d’être très simple à implémenter et d’avoir un calcul plutôt rapide pour un pas de temps donné, en comparaison avec d’autres méthodes d’intégration numérique (voir annexe)
Les inconvénients de la méthode d’Euler
La méthode d’intégration d’Euler présente un certain nombre de problèmes pour OSRD :
- Elle est relativement imprécise, et donc nécessite un faible pas de temps, ce qui génère beaucoup de données.
- En intégrant dans le temps, on ne connaît que les conditions du point de départ du pas d’intégration (pente, paramètres d’infrastructure, etc.) car on ne peut pas prédire précisément l’endroit où il se termine.
- On ne peut pas anticiper les futurs changements de directive : le train ne réagit qu’en comparant son état actuel à sa consigne au même instant. Pour illustrer c’est un peu comme si le conducteur était incapable de voir devant lui, alors que dans la réalité il anticipe en fonction des signaux, pentes, virages qu’il voit devant lui.
La méthode Runge-Kutta 4
La méthode Runge-Kutta 4 appliquée à l’intégration de l’équation du mouvement d’un train est :
$$v(t+dt) = v(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)dt$$
Avec :
$$k_1 = a(v(t), x(t))$$
$$k_2 = a\Big(v(t+k_1\frac{dt}{2}), x(t) + v(t)\frac{dt}{2} + k_1\frac{dt^2}{8}\Big)$$
$$k_3 = a\Big(v(t+k_2\frac{dt}{2}), x(t) + v(t)\frac{dt}{2} + k_2\frac{dt^2}{8}\Big)$$
$$k_4 = a\Big(v(t+k_3dt), x(t) + v(t)dt + k_3\frac{dt^2}{2}\Big)$$

Les avantages de la méthode de Runge Kutta 4
La méthode d’intégration de Runge Kutta 4 permet de répondre aux différents problèmes soulevés par celle d’Euler :
- Elle permet d’anticiper les changements de directive au sein d’un pas de calcul, représentant ainsi davantage la réalité de conduite d’un train.
- Elle est plus précise pour le même temps de calcul (voir annexe), permettant des étapes d’intégration plus grandes, donc moins de points de données.
Les inconvénients de la méthode de Runge Kutta 4
Le seul inconvénient notable de la méthode de Runge Kutta 4 rencontré pour l’instant est sa difficulté d’implémentation.
Le choix de la méthode d’intégration pour OSRD
Étude de la précision et de la vitesse de calcul
Différentes méthodes d’intégration auraient pu remplacer l’intégration d’Euler de base dans l’algorithme d’OSRD. Afin de décider quelle méthode conviendrait le mieux, une étude sur la précision et la vitesse de calcul de différentes méthodes a été menée. Cette étude sert à comparé les méthodes suivantes :
- Euler
- Euler-Cauchy
- Runge-Kutta 4
- Adams 2
- Adams 3
Toutes les explications sur ces méthodes peuvent être trouvées dans ce document, et le code python utilisé pour la simulation est ici.
La simulation calcule la position et la vitesse d’un TGV accélérant sur une ligne droite plate.
Simulations à pas de temps équivalent
Une courbe de référence a été simulée en utilisant la méthode d’Euler avec un pas de temps de 0,1s, puis le même parcours a été simulé en utilisant les autres méthodes avec un pas de temps de 1s. Il est alors possible de comparer simplement chaque courbe à la courbe de référence, en calculant la valeur absolue de la différence à chaque point calculé. Voici l’erreur absolue résultante de la position du train sur sa distance parcourue :

Il apparaît immédiatement que la méthode d’Euler est moins précise que les quatre autres d’environ un ordre de grandeur. Chaque courbe présente un pic où la précision est extrêmement élevée (erreur extrêmement faible), ce qui s’explique par le fait que toutes les courbes commencent légèrement au-dessus de la courbe de référence, la croisent en un point et finissent légèrement en dessous, ou vice versa.
Comme la précision n’est pas le seul indicateur important, le temps de calcul de chaque méthode a été mesuré. Voici ce que nous obtenons pour les mêmes paramètres d’entrée :
| Méthode d’intégration | Temps de calcul (s) |
|---|---|
| Euler | 1.86 |
| Euler-Cauchy | 3.80 |
| Runge-Kutta 4 | 7.01 |
| Adams 2 | 3.43 |
| Adams 3 | 5.27 |
Ainsi, Euler-Cauchy et Adams 2 sont environ deux fois plus lents que Euler, Adams 3 est environ trois fois plus lent, et RK4 est environ quatre fois plus lent. Ces résultats ont été vérifiés sur des simulations beaucoup plus longues, et les différents ratios sont maintenus.
Simulation à temps de calcul équivalent
Comme les temps de calcul de toutes les méthodes dépendent linéairement du pas de temps, il est relativement simple de comparer la précision pour un temps de calcul à peu près identique. En multipliant le pas de temps d’Euler-Cauchy et d’Adams 2 par 2, le pas de temps d’Adams 3 par 3, et le pas de temps de RK4 par 4, voici les courbes d’erreur absolue résultantes :

Et voici les temps de calcul :
| Méthode d’intégration | Temps de calcul (s) |
|---|---|
| Euler | 1.75 |
| Euler-Cauchy | 2.10 |
| Runge-Kutta 4 | 1.95 |
| Adams 2 | 1.91 |
| Adams 3 | 1.99 |
Après un certain temps, RK4 tend à être la méthode la plus précise, légèrement plus précise que Euler-Cauchy, et toujours bien plus précise que la méthode d’Euler.
Conclusions de l’étude
L’étude de la précision et de la vitesse de calcul présentée ci-dessus montre que RK4 et Euler-Cauchy seraient de bons candidats pour remplacer l’algorithme d’Euler dans OSRD : les deux sont rapides, précis, et pourraient remplacer la méthode d’Euler sans nécessiter de gros changements d’implémentation car ils ne font que des calculs au sein du pas de temps en cours de calcul. Il a été décidé qu’OSRD utiliserait la méthode Runge-Kutta 4 parce qu’elle est légèrement plus précise que Euler-Cauchy et que c’est une méthode bien connue pour ce type de calcul, donc très adaptée à un simulateur open-source.
3.3 - Le système d'enveloppes
Le système d’enveloppes est une interface créée spécifiquement pour le calcul de marche d’OSRD. Il permet de manipuler différentes courbes espace/vitesse, de les découper, de les mettre bout à bout, d’interpoler des points spécifiques, et d’adresser beaucoup d’autres besoins nécessaires au calcul de marche.
Une interface spécifique dans le service OSRD Core
Le système d’enveloppes fait partie du service core d’OSRD (voir l’architecture du logiciel).
Ses principaux composants sont :
1 - EnvelopePart : courbe espace/vitesse, définie comme une séquence des points et possédant des métadonnées indiquant par exemple s’il s’agit d’une courbe d’accélération, de freinage, de maintien de vitesse, etc.
2 - Envelope : liste d’EnvelopeParts mises bout-à-bout et sur laquelle il est possible d’effectuer certaines opérations :
- vérifier la continuité dans l’espace (obligatoire) et dans la vitesse (facultative)
- chercher la vitesse minimale et/ou maximale de l’enveloppe
- couper une partie de l’enveloppe entre deux points de l’espace
- effectuer une interpolation de vitesse à une certaine position
- calculer le temps écoulé entre deux positions de l’enveloppe

3 - Overlays : système permettant d’ajouter des EnvelopePart plus contraignantes (c’est-à-dire dont la vitesse est plus faible) à une enveloppe existante.
Enveloppes données vs enveloppes calculées
Pendant la simulation, le train est censé suivre certaines instructions de vitesse. Celles-ci sont modélisées dans OSRD par des enveloppes sous forme de courbes espace/vitesse. On en distingue deux types :
- Les enveloppes provenant des données d’infrastructure et de matériel roulant, comme la vitesse maximale de la ligne et la vitesse maximale du train. Etant des données d’entrée de notre calcul, elles ne correspondent pas à des courbes ayant un sens physique, car elles ne sont pas issues des résultats d’une intégration réelle des équations physiques du mouvement.
- Les enveloppes résultant d’une intégration réelle des équations du mouvement physique. Elles correspondent à une courbe physiquement tenable par le train et contiennent également des informations sur le temps.
Un exemple simple pour illustrer cette différence : si l’on simule un trajet de TER sur une ligne de montagne, une des données d’entrée va être une enveloppe de vitesse maximale à 160km/h, correspondant à la vitesse maximale de notre TER. Mais cette enveloppe ne correspond pas à une réalité physique, car il se peut que sur certaines portions la rampe soit trop raide pour que le train arrive effectivement à maintenir cette vitesse maximale de 160km/h. L’enveloppe calculée présentera donc dans cet exemple un décrochage de vitesse dans les zones de fortes rampes, là où l’enveloppe donnée était parfaitement plate.
Simulation de plusieurs trains
Dans le cas de la simulation de nombreux trains, le système de signalisation doit assurer la sécurité. L’effet de la signalisation sur le calcul de marche d’un train est reproduit en superposant des enveloppes dynamiques à l’enveloppe statique. Une nouvelle enveloppe dynamique est introduite par exemple lorsqu’un signal se ferme. Le train suit l’enveloppe économique statique superposée aux enveloppes dynamiques, s’il y en a. Dans ce mode de simulation, un contrôle du temps est effectué par rapport à un temps théorique provenant de l’information temporelle de l’enveloppe économique statique. Si le train est en retard par rapport à l’heure prévue, il cesse de suivre l’enveloppe économique et essaie d’aller plus vite. Sa courbe espace/vitesse sera donc limitée par l’enveloppe d’effort maximum.
3.4 - Le processus de calcul de marche
Le calcul de marche dans OSRD est un processus à 4 étapes, utilisant chacune le système d’enveloppes :
- Construction du profil de vitesse le plus restrictif
- Ajout des différentes courbes de freinage
- Ajout des différentes courbes d’accélération et vérification des courbes de vitesse constante
- Application de marge(s)
Calcul du profil de vitesse le plus restrictif
Une première enveloppe est calculée au début de la simulation en regroupant toutes les limites de vitesse statiques :
- vitesse maximale de la ligne
- vitesse maximale du matériel roulant
- limitations temporaires de vitesse (en cas de travaux sur une ligne par exemple)
- limitations de vitesse par catégorie de train
- limitations de vitesse selon la charge du train
- limitations de vitesse correspondant à des panneaux de signalisation
La longueur du train est également prise en compte pour s’assurer que le train n’accélère qu’une fois sa queue ayant quitté la zone de plus faible vitesse. Un décalage est alors appliqué à la courbe en pointillée rouge. L’enveloppe résultante (courbe noire) est appelée MRSP (Most Restricted Speed Profile) correspondant donc au profil de vitesse le plus restrictif. C’est sur cette enveloppe que seront calculées les étapes suivantes.

La ligne pointillée rouge représente la vitesse maximale autorisée en fonction de la position. La ligne noire représente le MRSP où la longueur du train a été prise en compte.
Il est à noter que les différentes envelopeParts composant le MRSP sont des données d’entrée, elles ne correspondent donc pas à des courbes avec une réalité physique.
Calcul du profil de vitesse maximale
En partant du MRSP, toutes les courbes de freinage sont calculées grâce au système d’overlay (voir ici pour plus de détails sur les overlays), c’est-à-dire en créant des envelopeParts qui seront plus restrictives que le MRSP. La courbe ainsi obtenue est appelée Max Speed Profile (profil de vitesse maximale). Il s’agit de l’enveloppe de vitesse maximale du train, tenant compte de ses capacités de freinage.
Etant donné que les courbes de freinage ont un point de fin imposé et que l’équation de freinage n’a pas de solution analytique, il est impossible de prédire leur point de départ. Les courbes de freinage sont donc calculées à rebours en partant de leur point cible, c’est-à-dire le point dans l’espace où une certaine limite de vitesse est imposée (vitesse cible finie) ou le point d’arrêt (vitesse cible nulle).

Pour des raisons historiques en production horaire, les courbes de freinages sont calculées avec une décélération forfaitaire, dite décélération horaire (typiquement ~0,5m/s²) sans prendre en compte les autres forces. Cette méthode a donc également été implémentée dans OSRD, permettant ainsi de calculer les freinages de deux manières différentes : avec ce taux horaire ou avec une force de freinage qui vient simplement s’ajouter aux autres forces.
Calcul du profil d’effort maximal
Pour chaque point correspondant à une augmentation de vitesse dans le MRSP ou à la fin d’une courbe de freinage d’arrêt, une courbe d’accélération est calculée. Les courbes d’accélération sont calculées en tenant compte de toutes les forces actives (force de traction, résistance à l’avancement, poids) et ont donc un sens physique.
Pour les envelopeParts dont le sens physique n’a pas encore été vérifié (qui à ce stade sont les phases de circulation à vitesse constante, provenant toujours du MRSP), une nouvelle intégration des équations de mouvement est effectuée. Ce dernier calcul est nécessaire pour prendre en compte d’éventuels décrochages de vitesse dans le cas où le train serait physiquement incapable de tenir sa vitesse, typiquement en présence de fortes rampes (voir cet exemple).
L’enveloppe qui résulte de ces ajouts de courbes d’accélérations et de la vérification des plateaux de vitesse est appelée Max Effort Profile (profil d’effort maximal).

A ce stade, l’enveloppe obtenue est continue et a un sens physique du début à fin. Le train accélère au maximum, roule aussi vite que possible en fonction des différentes limites de vitesse et de ses capacités motrices, et freine au maximum. Le calcul de marche obtenu s’appelle la marche de base. Elle correspond au trajet le plus rapide possible pour le matériel roulant donné sur le parcours donné.
Application de marge(s)
Après avoir effectué le calcul de la marche de base (correspondant au Max Effort Profile dans OSRD), il est possible d’y appliquer des marges (allowances). Les marges sont des ajouts de temps supplémentaire au parcours du train. Elles servent notamment à lui permettre de rattraper son retard si besoin ou à d’autres besoins opérationnels (plus de détails sur les marges ici).
Une nouvelle enveloppe Allowances est donc calculée grâce à des overlays pour distribuer la marge demandée par l’utilisateur sur l’enveloppe d’effort maximal calculée précédemment.

Dans le calcul de marche d’OSRD, il est possible de distribuer les marges d’une manière linéaire, en abaissant toutes les vitesses d’un certain facteur, ou économique, c’est-à-dire en minimisant la consommation d’énergie pendant le parcours du train.
3.5 - Les marges
La raison d’être des marges
Comme expliqué dans le calcul du Max Effort Profile, la marche de base représente la marche la plus tendue normalement réalisable, c’est-à-dire le trajet le plus rapide possible du matériel donné sur le parcours donné. Le train accélère au maximum, roule aussi vite que possible en fonction des différentes limites de vitesse et de ses capacités motrices, et freine au maximum.
Cette marche de base présente un inconvénient majeur : si un train part avec 10min de retard, il arrivera au mieux avec 10min de retard, car par définition il lui est impossible de rouler plus vite que la marche de base. Par conséquent, les trains sont programmés avec un ajout d’une ou de plusieurs marges. Les marges sont une détente du trajet du train, un ajout de temps à l’horaire prévu, qui se traduit inévitablement par un abaissement des vitesses de circulation.
Un train circulant en marche de base est incapable de rattraper son retard !
Le type de marge
On distingue deux types de marges :
- La marge de régularité : il s’agit du temps complémentaire ajouté à la marche de base pour tenir compte de l’imprécision de la mesure de la vitesse, pour pallier les conséquences des incidents extérieurs venant perturber la marche théorique des trains, et pour maintenir la régularité de la circulation. La marge de régularité s’applique sur l’ensemble du trajet, bien que sa valeur puisse changer sur certains intervalles.
- La marge de construction : il s’agit du temps ajouté / retiré sur un intervalle spécifique, en plus de la marge de régularité, mais cette fois pour des raisons opérationnelles (esquiver un autre train, libérer une voie plus rapidement, etc.)
Une marche de base à laquelle on vient ajouter une marge de régularité donne ce que l’on appelle une marche type.
La distribution de la marge
L’ajout de marge se traduisant par un abaissement des vitesses le long du trajet, plusieurs marches types sont possibles. En effet, il existe une infinité de solutions aboutissant au même temps de parcours.
En guise d’exemple simple, pour détendre la marche d’un train de 10% de son temps de parcours, il est possible de prolonger n’importe quel arrêt de l’équivalent en temps de ces 10%, tout comme il est possible de rouler à 1/1,1 = 90,9% des capacités du train sur l’ensemble du parcours, ou encore de rouler moins vite, mais seulement aux vitesses élevées…
Il y a pour l’instant deux algorithmes de distribution de la marge dans OSRD : linéaire et économique.
La distribution linéaire
La distribution de marge linéaire consiste simplement à abaisser les vitesses d’un même facteur sur la zone où l’utilisateur applique la marge. En voici un exemple d’application :

Cette distribution a pour avantage de répartir la marge de la même manière sur tout le trajet. Un train prenant du retard à 30% de son trajet disposera de 70% de sa marge pour les 70% de trajets restants.
La distribution économique
La distribution économique de la marge, présentée en détail dans ce document (MARECO est un algorithme conçu par la direction de la recherche SNCF), consiste à répartir la marge de la manière la plus économe possible en énergie. Elle est basée sur deux principes :
- une vitesse plafond, évitant les vitesses les plus consommatrices en énergie
- des zones de marche sur l’erre, situées avant les freinages et les fortes pentes, où le train circule à moteur coupé grâce à son inertie, permettant de ne consommer aucune énergie pendant ce laps de temps

Un exemple de marche économique. En haut, les pentes/rampes rencontrées par le train. Les zones de marche sur l’erre sont représentées en bleu.
4 - Netzgrafik-Editor
Netzgrafik-Editor (NGE) est un logiciel open-source qui permet la création, la modification et l’analyse d’horaires à intervalles réguliers, à un niveau de détail macroscopique, développé par les Chemins de Fer Fédéraux suisses (SBB CFF FFS). Voir les dépôts front-end et back-end.
OSRD et NGE sont sémantiquement différents: le premier fonctionne à un niveau de détail microscopique, est basé sur une infrastructure définie en qualité et représente une grille horaire composée d’instances uniques de trains, alors que le second fonctionne à un niveau de détail macroscopique, sans infrastructure explicite et représente un plan de transport composé de lignes de train cadencées. Cependant, ces différences, suffisamment proches, peuvent être manipulées pour fonctionner ensemble.
La compatibilité entre NGE et OSRD a été testée à travers une preuve de concept, en exécutant les deux applications comme services distincts sans synchronisation automatisée.
L’idée est de fournir à OSRD un outil graphique pour éditer (créer, mettre à jour et supprimer les horaires des trains) une grille horaire à partir d’un scénario d’étude opérationnelle, et obtenir en même temps des informations analytiques. Utiliser des niveaux de détail microscopique et macroscopique permet un second bénéfice : les calculs microscopiques d’OSRD étendent le périmètre de NGE, ses fonctionnalités et les informations fournies, comme par exemple les simulations microscopiques ou l’outil de détection de conflits.
L’objectif transversal de cette fonctionnalité est de faire collaborer deux projets open-source de deux grands gestionnaires d’infrastructure ferroviaire pour atteindre le même objectif, celui d’assurer une continuité numérique à différentes échelles temporelles pour les études d’exploitations ferroviaires.
1 - Intégration dans OSRD
OSRD a développé une version standalone de NGE, intégrée au code source, qui permet à NGE de fonctionner sans back-end. Ainsi, à des fins d’utilisation externe, un build de NGE standalone est disponible sur NPM, et est publié à chaque release. Enfin, pour répondre à des besoins spécifiques à OSRD, OSRD utilise un fork de NGE (dont le build, NGE standalone, est aussi disponible sur NPM), en restant le plus proche possible du répertoire officiel.
Malgré l’utilisation de frameworks JavaScript différents (ReactJS pour OSRD et Angular pour NGE), ce build permet à OSRD d’intégrer NGE au sein d’un iframe. Cet iframe instancie un Custom Element, qui est l’interface de communication entre les deux applications et démarre le build de NGE.
Une alternative pour répondre au problème d’intégration aurait été de réécrire NGE en web-components, pour les importer dans OSRD, mais cette solution a été abandonnée compte tenu de la quantité de travail que cela représenterait.
NGE, sous sa version standalone, communique avec OSRD à travers l’iframe grâce à des propriétés d’éléments du DOM :
@Input: avec la propriéténetzgrafikDto, déclenchée à la mise à jour du contenu du scénario depuis OSRD.@Output: avec la propriétéoperations, déclenchée à l’utilisation de NGE.
NGE est alors capable d’obtenir la grille horaire OSRD dès qu’un changement est effectué du côté d’OSRD, et OSRD est capable d’obtenir les modifications effectuées du côté de NGE.
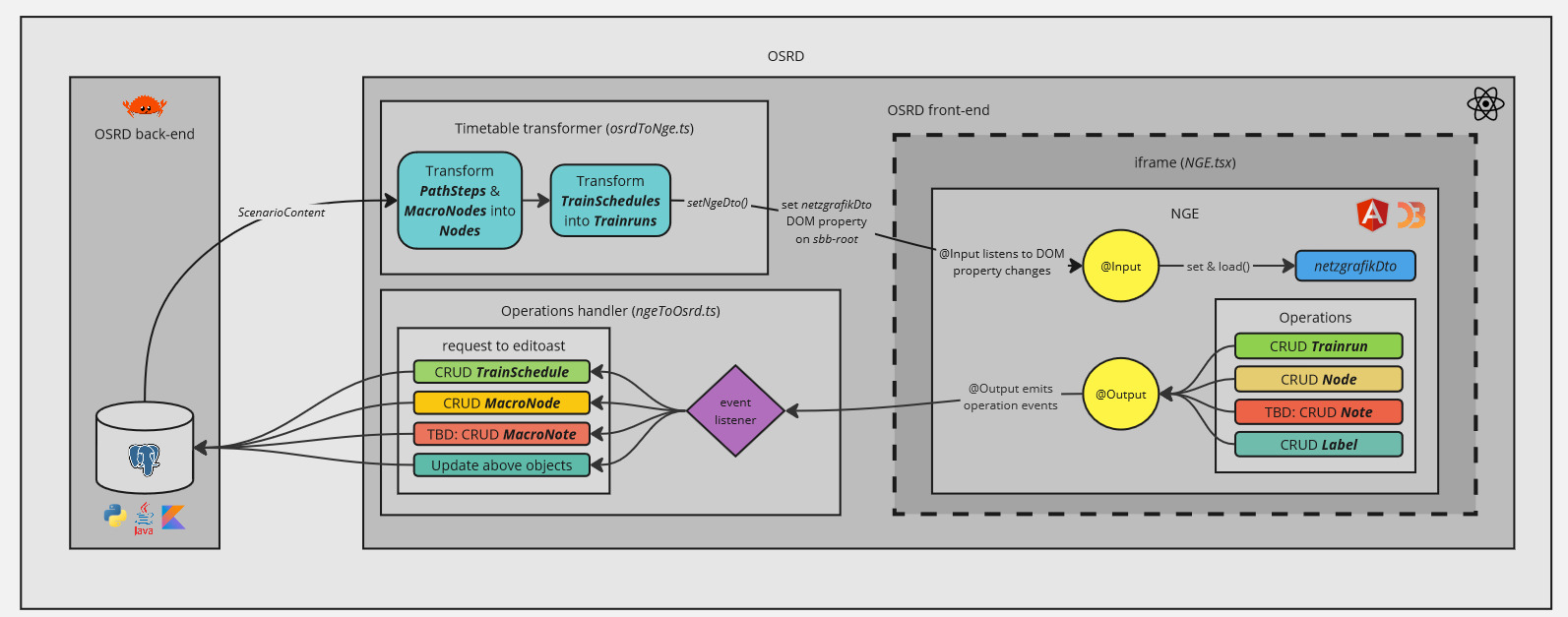
Il est important de noter que dans sa version standalone, NGE se repose alors ici sur le front-end d’OSRD, lui-même mis à jour par le back-end d’OSRD. De nouvelles tables en base de données, des modifications et de nouvelles routes sont alors nécessaires pour persister les informations macroscopiques d’un scénario.
2 - Convertisseurs
Pour surpasser les différences sémantiques et adapter les modèles de données, deux convertisseurs sont implémentés :
- [OSRD -> NGE] un convertisseur qui transforme une grille horaire OSRD en un modèle NGE. Les nœuds sont les points de passage décrits par les circulations, et dont les informations macroscopiques (position sur le réticulaire) sont stockés en base de données. Les circulations OSRD,
TrainSchedule, représentent alors des lignes de train cadencées dans NGE,Trainrun. Un concept de lignes de trains cadencées, sera bientôt implémenté pour permettre la convergence conceptuelle entre OSRD et NGE. - [OSRD <- NGE] un gestionnaire d’événements, qui transforme une action NGE en mise à jour de la base de données OSRD.
3 - Open-source (coopération / contribution)
Pour rendre NGE compatible avec OSRD, certaines modifications ont été demandées (désactivation du back-end, création de hooks sur les événements) et directement implémentées dans le répertoire officiel de NGE, avec l’accord et l’aide de l’équipe NGE.
Les contributions d’un projet à l’autre, de part et d’autre, sont précieuses et seront encouragées à l’avenir.
Cette fonctionnalité montre également que la coopération open-source est puissante et constitue un gain de temps considérable dans le développement de logiciels.