Encoding the solution space

General principle

The problem is still a pathfinding problem in a given graph. Once the problem is encoded as a graph search, it is possible to reuse our existing tools for this purpose.

We consider the product graph of position, time, and speed. This means that every graph element contains these 3 variables (among other things)

Every graph edge is computed using running-time calculation to get speed and positions as functions of time.

Graphical representation

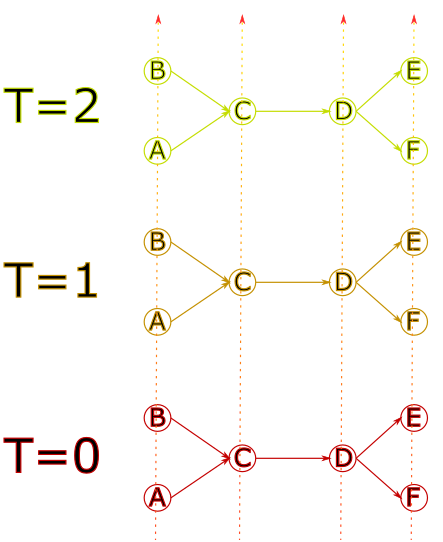
Space is encoded with a graph that contains the physical infrastructure.

It is then “duplicated” at different times.

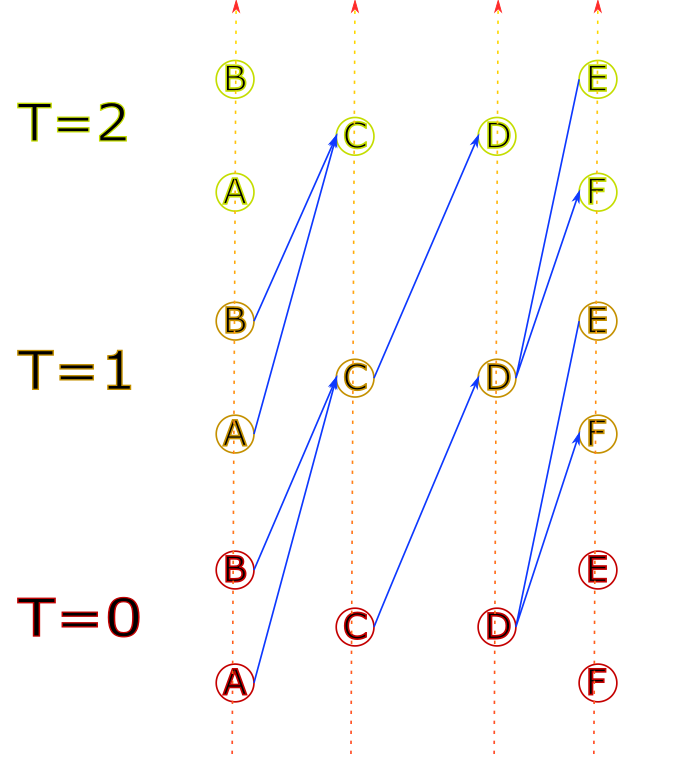
The nodes are then linked together in a way that reflects travel time.

Notes

• The graph is constructed on the fly as it is explored.
• It is discretized in time, to evaluate which nodes have already been visited. We keep full accuracy of time values, but two nodes at the same place and close times are considered identical.
• Every edge is computed with a running time computation.
• Speed isn’t discretized or considered to check visited nodes, it’s only used to compute time.
• By default, the train always goes as fast as it can (while still following standard allowances). It only slows down when necessary.

Example

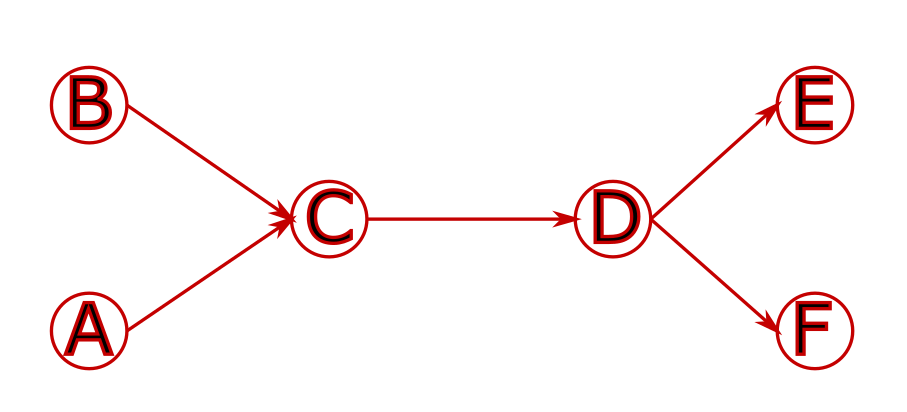
For example, with the following infrastructure, using the track graph:

Exploring the solution graph can give the following result: