Train slot search module

• 1: Input format
• 2: Encoding the solution space
• 3: Discontinuities and backtracking
• 4: Conflict avoidance
• 5: Standard allowance
• 6: Implementation details

1 - Input format

This module takes several parameters to find a path:

• A graph describing the physical infrastructure
• Unavailable sections in time intervals
• Origin and destination point(s)
• Departure time interval
• Maximum run time
• Simulation parameters (rolling stock, time step, allowances, …)

Among those, the first 3 require more explanations.

Infrastructure graph

Today, the input graph is the SignalingRoutes graph. But it can be any graph that represents the physical infrastructures and the paths that can be used.

The only constraints are: the edges must have a length, and it must be possible to compute running time on parts of an edge.

Unavailable sections

This input encodes the areas that are unavailable because of capacity constraints.

Every edge has a set of “occupancy block”. A block is made of these elements:

• Start offset
• End offset
• Start time
• End time

Offsets are relative to the start of the edge. Each block means that the head of the train cannot be located in the edge segment during the given interval.

These blocks include the grid margin. If the solution needs to have an x seconds margin before the train passage, every block ends x seconds later.

To give an example, with the following schedule, a 42m long train, and 10m sight distance:

• The occupancy of the block 1 from t=0 to t=300 makes it unavailable in its entirety during this time
• The last 10 meters of block 1 are unavailable from t=300 to t=360, because the signal at the start of block 2 must be green when the conductor sees it. It is possible to consider that this unavailability block starts at t=130 (when the next signal isn’t green), as blocks can overlap.
• The occupancy of block 2 from t=130 to t=360 makes it unavailable during this time. It is also unavailable from t=0, as the presence of a train in this block would cause a warning on block 1.
• The first 42 meters of block 3 are unavailable from t=0 to t=360, because the tail of the train must have left the block 2 at this time.
• The rest of block 3 is unavailable in its entirety from t=280 to t=360

2 - Encoding the solution space

General principle

The problem is still a pathfinding problem in a given graph. Once the problem is encoded as a graph search, it is possible to reuse our existing tools for this purpose.

We consider the product graph of position, time, and speed. This means that every graph element contains these 3 variables (among other things)

Every graph edge is computed using running-time calculation to get speed and positions as functions of time.

Graphical representation

Space is encoded with a graph that contains the physical infrastructure.

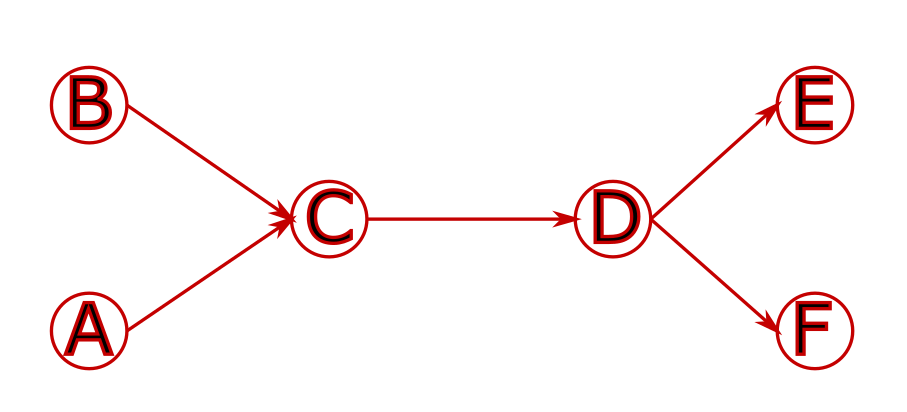
It is then “duplicated” at different times.

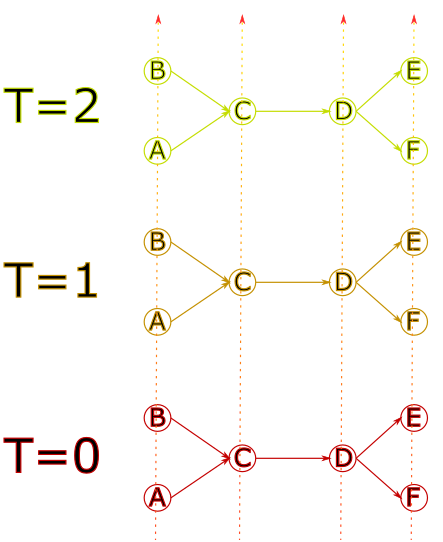
The nodes are then linked together in a way that reflects travel time.

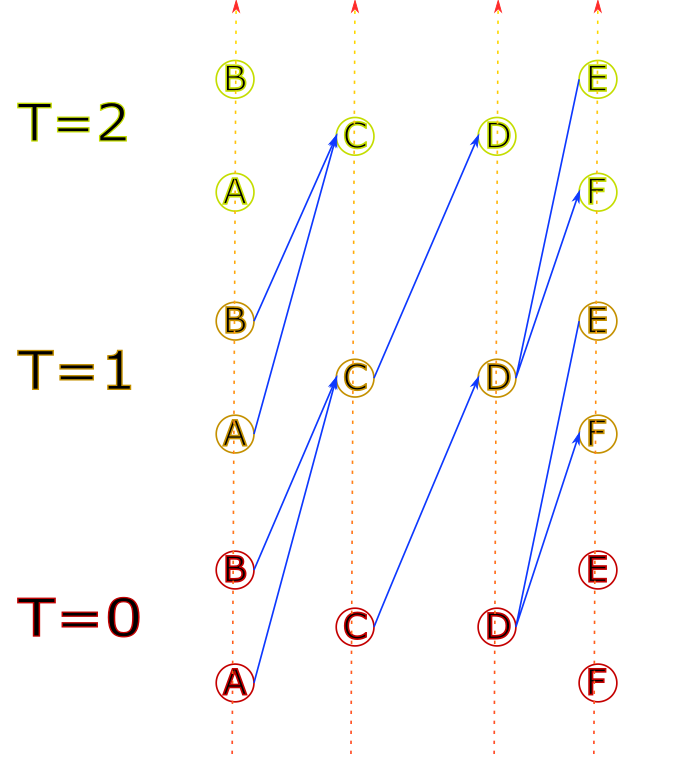
Notes

• The graph is constructed on the fly as it is explored.
• It is discretized in time, to evaluate which nodes have already been visited. We keep full accuracy of time values, but two nodes at the same place and close times are considered identical.
• Every edge is computed with a running time computation.
• Speed isn’t discretized or considered to check visited nodes, it’s only used to compute time.
• By default, the train always goes as fast as it can (while still following standard allowances). It only slows down when necessary.

Example

For example, with the following infrastructure, using the track graph:

Exploring the solution graph can give the following result:

3 - Discontinuities and backtracking

The discontinuity problem

When a new graph edge is visited, a simulation is run to evaluate its speed. But it is not possible to see beyond the current edge. This makes it difficult to compute braking curves, because they can span over several edges.

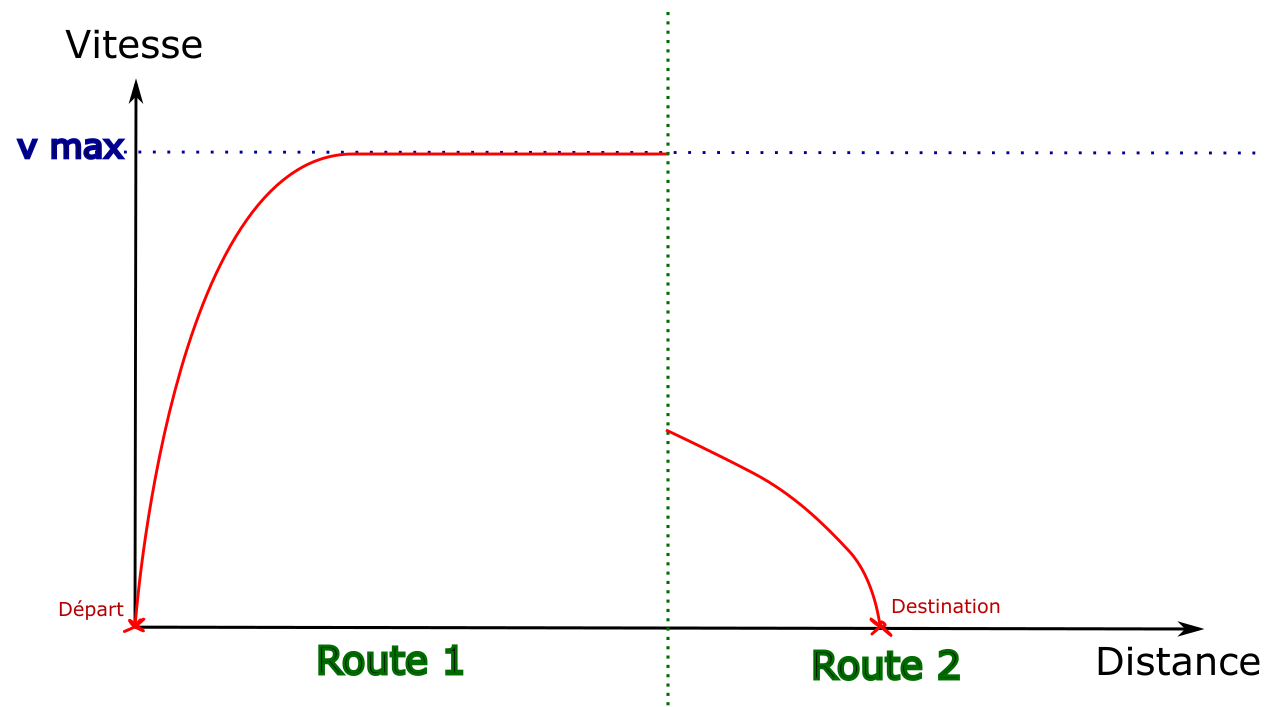
This example illustrates the problem: by default the first edge is explored by going at maximum speed. The destination is only visible once the second edge is visited, which doesn’t leave enough distance to stop.

Solution : backtracking

To solve this problem, when an edge is generated with a discontinuity in the speed envelopes, the algorithm goes back over the previous edges to create new ones that include the decelerations.

To give a simplified example, on a path of 4 edges where the train can accelerate or decelerate by 10km/h per edge:

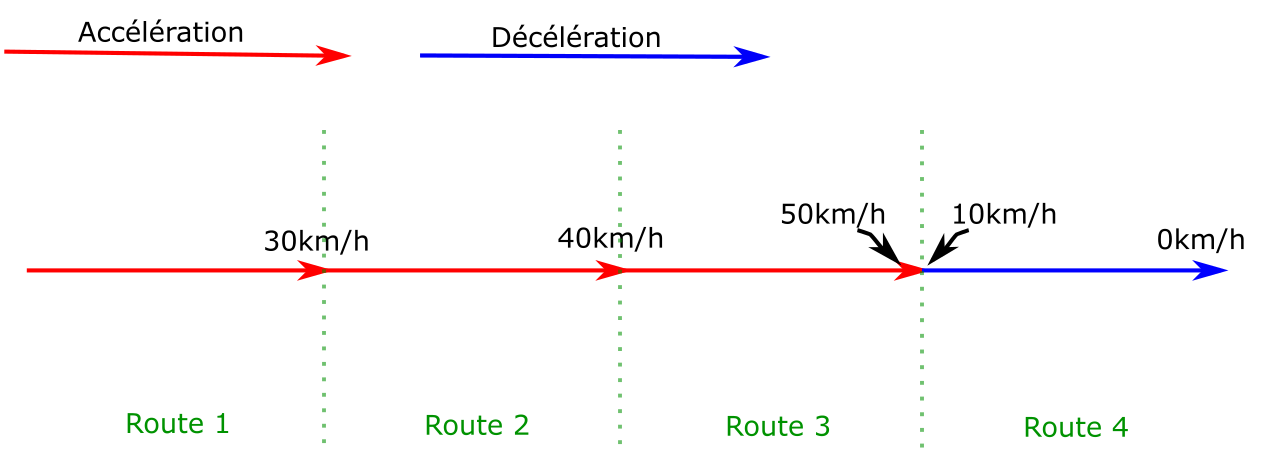
For the train to stop at the end of route 4, it must be at most at 10km/h at the end of edge 3. A new edge is then created on edge 3, which ends at 10km/h. A deceleration is computed backwards from the end of the edge back to the start, until the original curve is met (or the start of the edge).

In this example, the discontinuity has only been moved to the transition between edges 2 and 3. The process is then repeated on edge 2, which gives the following result:

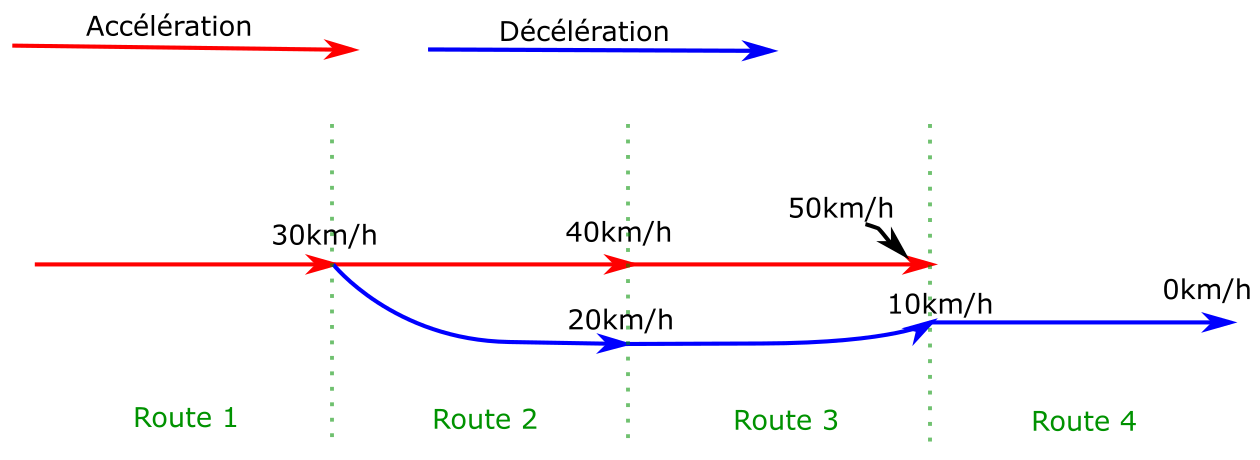
Old edges are still present in the graph as they can lead to other solutions.

4 - Conflict avoidance

While exploring the graph, it is possible to end up in locations that would generate conflicts. They can be avoided by adding delay.

Shifting the departure time

The departure time is defined as an interval in the module parameters: the train can leave at a given time, or up to x seconds later. Whenever possible, delay should be added by shifting the departure time.

for example : a train can leave between 10:00 et 11:00. Leaving at 10:00 would cause a conflict, the train actually needs to enter the destination station 15 minutes later. Making the train leave at 10:15 solves the problem.

In OSRD, this feature is handled by keeping track, for every edge, of the maximum duration by which we can delay the departure time. As long as this value is enough, conflicts are avoided this way.

This time shift is a value stored in every edge of the path. Once a path is found, the value is summed over the whole path. This is added to the departure time.

For example :

• a train leaves between 10:00 and 11:00. The initial maximum time shift is 1:00.
• At some point, an edge becomes unavailable 20 minutes after the train passage. The value is now at 20 for any edge accessed from here.
• The departure time is then delayed by 5 minutes to avoid a conflict. The maximum time shift value is now at 15 minutes.
• This process is applied until the destination is found, or until no more delay can be added this way.

Engineering allowances

Once the maximum delay is at 0, the delay needs to be added between two points of the path.

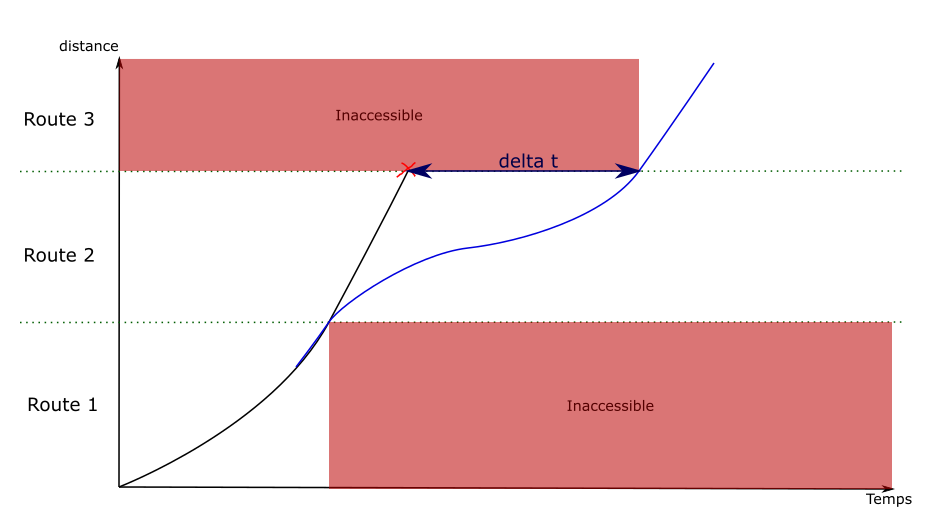
The idea is the same as the one used to fix speed discontinuities: new edges are created, replacing the previous ones. The new edges have an engineering allowance, to add the delay where it is possible.

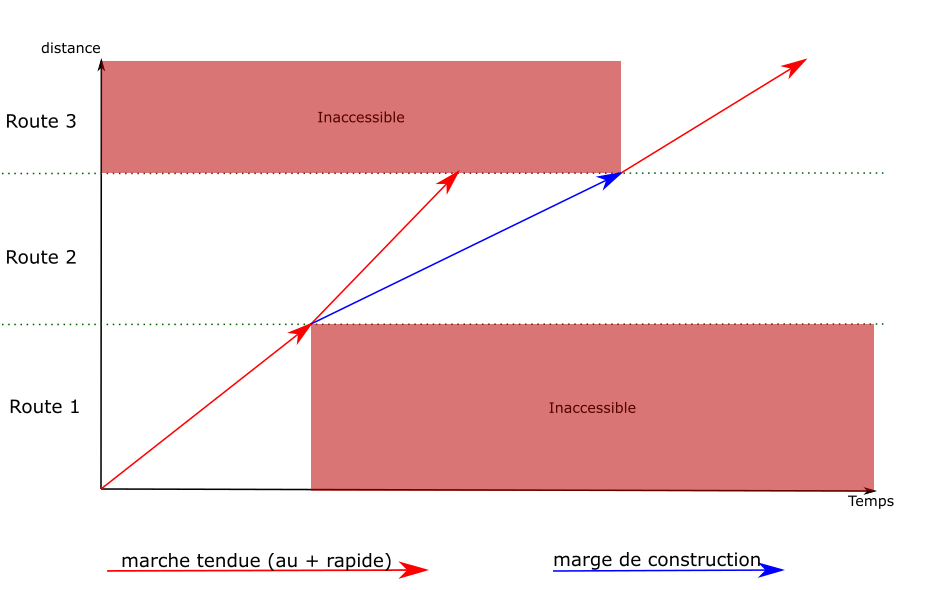
computing an engineering allowance is a feature of the running-time calculation module. It adds a given delay between two points of a path, without affecting the speeds on the rest of the path.

5 - Standard allowance

The STDCM module must be usable with standard allowances. The user can set an allowance value, expressed either as a function of the running time or the travelled distance. This time must be added to the running time, so that it arrives later compared to its fastest possible running time.

For example: the user can set a margin of 5 minutes per 100km. On a 42km long path that would take 10 minutes at best, the train should arrive 12 minutes and 6 seconds after leaving.

This can cause problems to detect conflicts, as an allowance would move the end of the train slot to a later time. The allowance must be considered when we compute conflicts as the graph is explored.

The allowance must also follow the MARECO model: the extra time isn’t added evenly over the whole path, it is computed in a way that requires knowing the whole path. This is done to optimize the energy used by the train.

Linear margin expressed as a function of time

As a first step, the problem is solved with a linear margin, i.e. added evenly over the whole path. The speed is simply modified by a constant factor.

The envelopes. computed during the graph traversal are not modified, they are always at maximum speed. But they are paired with a speed factor, which is used to compute running time and to evaluate conflicts.

The final envelope, with the allowance, is only computed once a path is found.

Linear margin expressed as a function of distance

The principle is generally the same, but with an extra difficulty: the speed factor isn’t constant over the path. When a train goes faster, it travels more distance in the same time, which increases the allowance time and the speed factor.

Because the train speed changes over the path, the speed factor changes from one edge to another. This causes irregular speed curves.

MARECO Allowances

This is exclusively a post-processing step, because it isn’t possible to compute the MARECO envelope without knowing the full train path. When looking for a path, linear allowances are used.

This means that conflicts may appear at this step. To avoid them, the following procedure is applied:

1. A mareco allowance is applied over the whole path.
2. If there are conflict, the first one is considered.
3. The mareco allowance is split in two intervals. The point where the first conflict appeared is set to be at the same time as the envelope with a linear allowance, removing the conflict at this point.
4. This process is repeated iteratively until no conflict is found.

6 - Implementation details

This page is about implementation details. It isn’t necessary to understand general principles, but it helps before reading the code.

STDCMEdgeBuilder

This refers to this class in the project.

This class is used to make it easier to create instances of STDCMEdge, the graph edges. Those contain many attributes, most of which can be determined from the context (e.g. the previous node). The STDCMEdgeBuilder class makes some parameters optional and automatically computes others.

Once instantiated and parametrized, an STDCMEdgeBuilder has two methods:

• Collection<STDCMEdge> makeAllEdges() can be used to create all the possible edges in the given context for a given route. If there are several “openings” between occupancy blocks, one edge is instantiated for each opening. Every conflict, their avoidance, and their related attributes are handled here.

• STDCMEdge findEdgeSameNextOccupancy(double timeNextOccupancy): This method is used to get the specific edges that uses a certain opening (when it exists), identified here with the time of the next occupancy block. It is called whenever a new edge must be re-created to replace an old one. It calls the previous method.

Pathfinding

The methods mentioned here are defined in this class.

Cost function

The function used to define pathfinding cost sets which path is used over another. The result is always the one that minimizes this cost (as long as the heuristic is admissible).

Here, two parameters are used: total run time and departure time. The latter has a very small weight compared to the former, so that the fastest path is found. More details are explained in the documentation of those methods.

Heuristics

The algorithm used to find a path is an A*, with a heuristic based on geographical coordinates.

However, the coordinates of generated infrastructures are arbitrary and don’t reflect the track distance. It means that, for the generated infrastructures, the path may not always be the shortest one.

It would be possible to use this heuristic to determine whether the current node can lead to a path that doesn’t take longer than the maximum allowed total run time. But for the same reason, adding this feature would break any STDCM test on generated infras. More details in this issue.